논리회로 (logic circuit)
조합회로(combinational circuit)
- Boole 함수의 집합을 논리적으로 구현하는 동작을 수행
- 출력이 입력값에 따라 결정됨
순차회로(sequential circuit)
- 출력이 저장된 값과 입력 값에 따라 달라짐.
- 출력 값이 현재 입력 값 뿐만 아니라 이전 입력값에 따라 달라짐.
- 회로의 동작을 입력 값과 저장된 값의 시간순서로 정의할 수 있음.
조합회로
조합회로
• 출력값이 현재의 입력값에 의해 결정됨
• 입력변수와 논리 게이트, 출력 변수들로 구성됨

n개의 입력변수에 대해 2^n개의 2진 입력조합이 가능
각 입력조합에 대하여 하나의 출력
출력 변수 하나를 Boole 함수로 표현할 수 있음.
디지털 시스템을 설계하는데 자주 사용되는 조합회로들
가산기, 감산기, 비교기, 디코더, 인코더, 곱셈기
- 집적회로에서 MSI(Medium scale integration)회로로 이용 가능
- ASIC(Application specific integrated circuits)와 같은 복잡한 VLSI 회로에서 표준 셀 (standard cell)로 이용됨
분석과정
조합회로의 분석
회로가 수행하는 기능을 결정하는 과정
분석 절차
1. 회로가 조합 회로인지 순차 회로인지 확인한다.
-> 귀환경로나 저장장치가 있는지 확인. 존재하면 조합회로가 아니다.
※귀환경로: 한 게이트의 출력이 첫번째 게이트의 입력으로 연결된 경로
2. 출력단의 Boole 함수 또는 진리표를 구한다.
유도과정
Boole 함수를 구하는 과정
1. 모든 게이트의 출력에 기호를 붙인다.
2. 각 게이트의 출력에 대한 Boole함수를 구한다.
3. 최종 출력에 입력 변수들을 대입한다.
진리표
1. 입력 변수들을 2진수로 놓는다.
2. 각각의 게이트에 해당하는 출력값을 결정한다.
3. 진리표를 구한다.
참고: 진리표 -> 회로도 (설계과정) / 회로도 -> 진리표 (분석과정)
Boole 함수 유도과정

T2=ABC
T1=A+B+C
F2=AB+AC+BC
T3=F2’T1
F1=T3+T2
=A’BC’+A’B’C+AB’C’+ABC
진리표 유도과정

설계과정
조합회로의 설계
설계사양(specification)을 명시하고 논리도표나 Boole 함수의 집합을 구해야 함.
설계 절차
1. 설계 사양으로부터 필요한 입/출력의 개수를 정한다.
2. 각각의 입/출력에 대하여 문자 기호를 붙인다.
3. 입/출력간의 관계를 정의하는 진리표를 구한다.
4. 간략화된 Boole 함수를 유도한다.
5. 논리도표를 그리고 설계의 정확성을 검증한다.

코드 변환 조합회로
> 코드 변환의 필요성
한 시스템의 출력이 다른 시스템의 입력이 되는 경우 있음.
각 시스템이 동일한 정보에 대하여 다른 코드를 사용하고 있다면 두 시스템간에는 변환 회로가 필요
> 코드 변환기
각 시스템이 다른 2진 코드를 사용하고 있더라도 호환 가능하도록 해주는 회로
설계 예시1 : BCD to excess-3 코드 변환기
※ Excess-3 code : 10진값에 3을 더한 2진 코드
설계 절차
(1) 입력과 출력의 결정
입력 : A,B,C,D (0000∼1001)
출력 : W,X,Y,Z (0011∼1100)
(2) 진리표 구하기 ※ 출력이 명시되지 않은 비트는 Don't Care Condition에 해당함

(3) 간략화된 Boole 함수 구하기
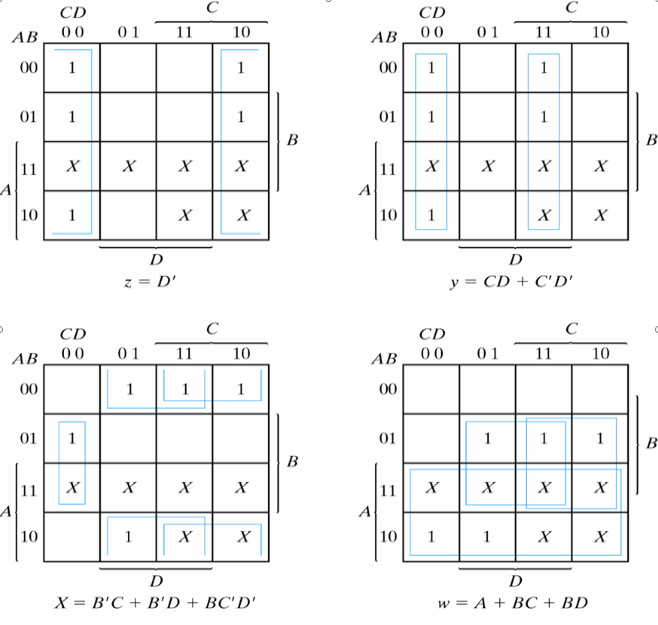
(4) 논리도 그리기


설계 예시2 : Excess-3 to 8 4 -2 -1 코드 변환기
※ 8 4 -2 -1 : 각 비트의 값이 8, 4, -2, -1인 코드
설계 절차
(1) 입력과 출력의 결정
입력 : A,B,C,D (0011∼1100) # Excess-3 코드이므로 0011은 Digit 0에 해당함
출력 : W,X,Y,Z (0000∼1111)
(2) 진리표 구하기 ※ 출력이 명시되지 않은 비트(X)는 Don't Care Condition에 해당함
A B C D | w x y z
-----------------
0 0 0 0 | X X X X
0 0 0 1 | X X X X
0 0 1 0 | X X X X
0 0 1 1 | 0 0 0 0
0 1 0 0 | 0 1 1 1
0 1 0 1 | 0 1 1 0
0 1 1 0 | 0 1 0 1
0 1 1 1 | 0 1 0 0
1 0 0 0 | 1 0 1 1
1 0 0 1 | 1 0 1 0
1 0 1 0 | 1 0 0 1
1 0 1 1 | 1 0 0 0
1 1 0 0 | 1 1 1 1
1 1 0 1 | X X X X
1 1 1 0 | X X X X
1 1 1 1 | X X X X(3) 간략화된 Boole 함수 구하기

(4) 논리도 그리기
생략
2진 가산기와 감산기
2진 가산기
반가산기 : 2비트를 더하는 기능 수행 (x+y)
가산기 : 3비트를 더하는 기능 수행 (x+y+z)
2개의 반가산기는 하나의 가산기로 쓸 수 있음.
2진 가산기 – 감산기의 구현
단계적 설계
- 가산기
- n개 가산기의 직렬 연결
- 보수회로의 추가
반가산기
2개의 2진 입력의 합
2개의 2진 입력과 2개의 2진 출력
입력 : X(피가산수), Y(가산수)
출력 : S(sum), C(carry)


가산기
3개의 2진 입력의 합
입력 : X,Y(2개의 유효비트),Z(하나의 캐리비트)
출력 : S(sum),C(carry)




2진 가산기 (두 n비트 2진수의 합)
예제 ) 4비트 가산기
A=1011, B=0011


설계 예시1 - 2진 가산기 (AB + CD)
설계 절차
(1) 입력비트: A, B, C, D / 출력비트: x, y, z
(2) 진리표
A B C D | x y z
---------------
0 0 0 0 | 0 0 0
0 0 0 1 | 0 0 1
0 0 1 0 | 0 1 0
0 0 1 1 | 0 1 1
0 1 0 0 | 0 0 1
0 1 0 1 | 0 1 0
0 1 1 0 | 0 1 1
0 1 1 1 | 1 0 0
1 0 0 0 | 0 1 0
1 0 0 1 | 0 1 1
1 0 1 0 | 1 0 0
1 0 1 1 | 1 0 1
1 1 0 0 | 0 1 1
1 1 0 1 | 1 0 0
1 1 1 0 | 1 0 1
1 1 1 1 | 1 1 0(3) 간략화된 Boole 함수
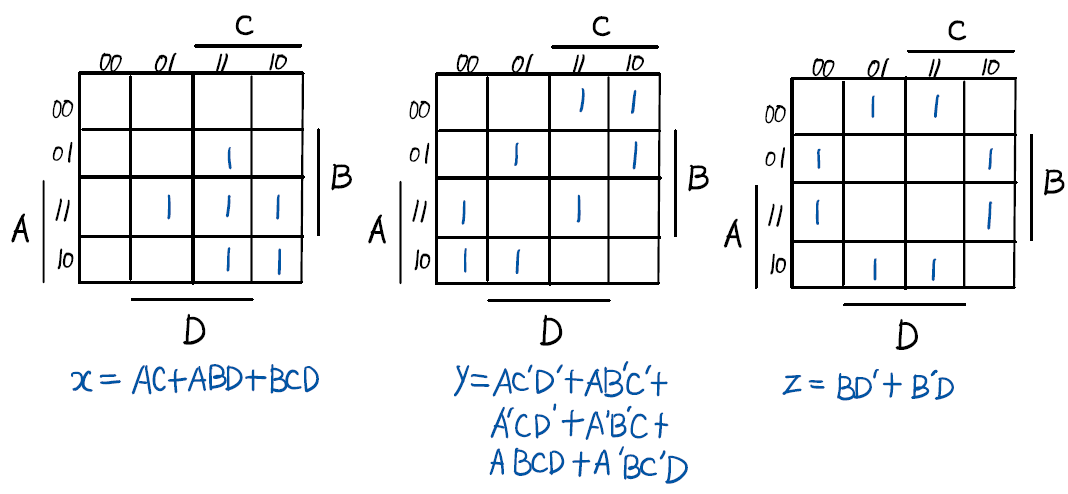
(4) 논리도 그리기
생략
설계 예시2 - 2비트 비교기
설계 절차
(1) 입력비트 A, B, C, D에 대하여 A, B와 C, D중
input : A, B > C, D output : x = 0 y = 1
input : A, B < C, D output : x = 0 y = 0
input : A, B = C, D output : x = 1 y = Don't Care Condition
(2) 진리표
A B C D | x y
-------------
0 0 0 0 | 1 X
0 0 0 1 | 0 0
0 0 1 0 | 0 0
0 0 1 1 | 0 0
0 1 0 0 | 0 1
0 1 0 1 | 1 X
0 1 1 0 | 0 0
0 1 1 1 | 0 0
1 0 0 0 | 0 1
1 0 0 1 | 0 1
1 0 1 0 | 1 X
1 0 1 1 | 0 0
1 1 0 0 | 0 1
1 1 0 1 | 0 1
1 1 1 0 | 0 1
1 1 1 1 | 1 X(3) 간략화된 Boole 함수

(4) 논리도 그리기
생략
설계 예시3 - 2진 곱셈기 (AB * CD)
설계 절차
(1) 입력비트: A, B, C, D / 출력비트: w, x, y, z
(2) 진리표
A B C D | w x y z
-----------------
0 0 0 0 | 0 0 0 0
0 0 0 1 | 0 0 0 0
0 0 1 0 | 0 0 0 0
0 0 1 1 | 0 0 0 0
0 1 0 0 | 0 0 0 0
0 1 0 1 | 0 0 0 1
0 1 1 0 | 0 0 1 0
0 1 1 1 | 0 0 1 1
1 0 0 0 | 0 0 0 0
1 0 0 1 | 0 0 1 0
1 0 1 0 | 0 1 0 0
1 0 1 1 | 0 1 1 0
1 1 0 0 | 0 0 0 0
1 1 0 1 | 0 0 1 1
1 1 1 0 | 0 1 1 0
1 1 1 1 | 1 0 0 1(3) 간략화된 Boole 함수

(4) 논리도 그리기
생략
자료참조 - Digital Design 6th Morris Mano
'컴퓨터공학 💻 > 디지털 시스템 회로 설계' 카테고리의 다른 글
| [디지털 시스템 회로 설계] 순차논리회로 분석 및 설계 (0) | 2021.11.05 |
|---|---|
| [디지털 시스템 회로 설계] 디코더, 인코더, 멀티플렉서, 디멀티플렉서 (0) | 2021.10.27 |
| [디지털 시스템 회로 설계] NAND 게이트, NOR 게이트 구현, Exclusive-OR 함수 (0) | 2021.10.16 |
| [디지털 시스템 회로 설계] 디지털 논리게이트와 게이트 레벨 최소화(카르노맵) (0) | 2021.10.03 |
| [디지털 시스템 회로 설계] 부울 대수와 논리게이트 (0) | 2021.09.17 |