NAND 게이트, NOR 게이트 구현, Exclusive-OR 함수
디지털 회로는 AND나 OR 게이트보다는 대개 NAND와 NOR 게이트를 이용하여 구현됨.
NAND와 NOR 게이트는 회로적으로 구성되기 쉽기 때문에 모든 IC 디지털 논리 회로군의 기본 게이트로 사용됨.
AND, OR, NOT으로 주어지는 Boole 함수를 등가의 NAND와 NOR로 구성된 논리 도표로 변환할 수 있는 법칙과 과정 개발됨
NAND 회로
NAND 게이트로 된 Boole 함수의 구현을 위해서는 곱의 합 형태로 만들어야 함.
 Two graphic symbols for a three-input NAND gate
Two graphic symbols for a three-input NAND gate
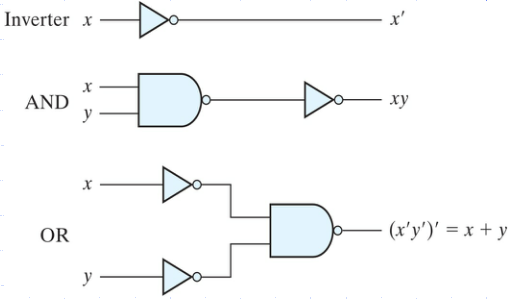 Logic operations with NAND gates
Logic operations with NAND gates
다중 레벨 AND-OR 논리 도표를 NAND 논리 도표로 변환
- 모든 AND 게이트를 AND-invert로 바꾼다.
- 모든 OR 게이트를 invert-OR로 바꾼다.
- 논리 도표의 모든 버블을 검사
상쇄되지 않는 버블들이 있으면 인버터(단입력 NAND 게이트)를 넣거나 입력 리터럴을 보수화
예제
F = ((AB)'(CD)')' = AB + CD
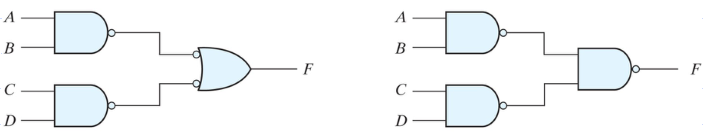
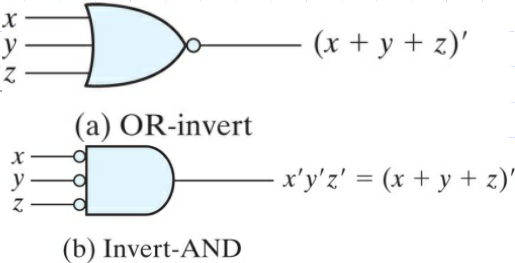
F(x, y, z) = Σ(1, 2, 3, 4, 5, 7) = xy' + x'y + z

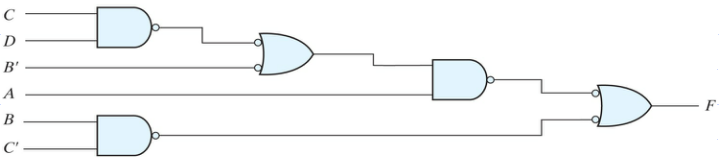
F = A(CD + B) + BC’
NOR 회로
 Two graphic symbols for the NOR gate
Two graphic symbols for the NOR gate
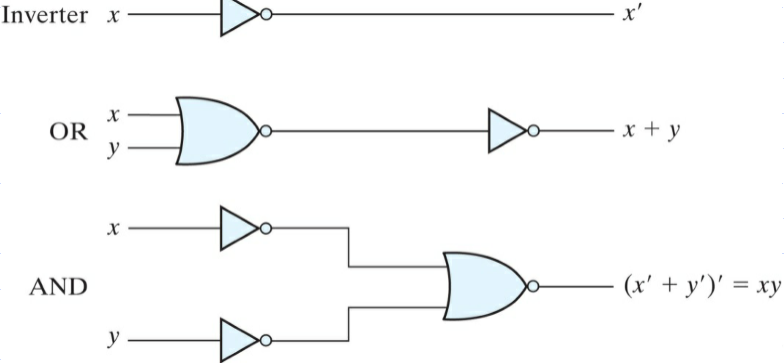 Logic operations with NOR gates
Logic operations with NOR gates
예제
F = (A + B)(C + D)E

F = (AB’ + A’B)(C + D’)

연습문제 (NAND 회로)
다음 함수들을 간략한 두단계 NAND 게이트 회로도로 그려라.
F(A,B,C,D)=Σ(0, 2,4,6,9, 10,15)
F(A,B,C,D) = ∏(0, 1, 2, 4, 5, 6, 7, 8, 10, 11, 12, 14, 15)
Don`t care 조건, d(A,B,C,D) = Σ(13, 14) 을 갖는 다음 Boole 함수를 간략한 두단계 NAND 게이트 회로도로 그려라.
F(A,B,C,D) = Σ(0, 1, 2, 3, 7, 11, 12, 15)
연습문제 (NOR 회로)
다음 함수들을 간략한 두단계 Nor 게이트 회로도로 그려라.
F(A,B,C,D) = Σ(0,2,9,12,13,15)
F(A,B,C,D) = ∏(1, 2, 4, 5, 6, 9, 10, 11, 12)
Don`t care 조건, d(A,B,C,D) = Σ(11, 15) 을 갖는 다음 Boole 함수를 간략한 두단계 Nor 게이트 회로도로 그려라.
F(A,B,C,D) = Σ(1,3,7,8,9,10,12,14)
Exclusive-OR 함수
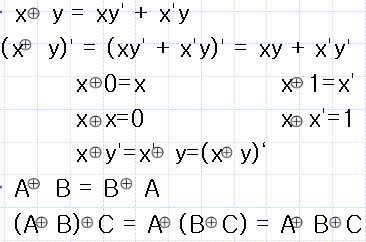
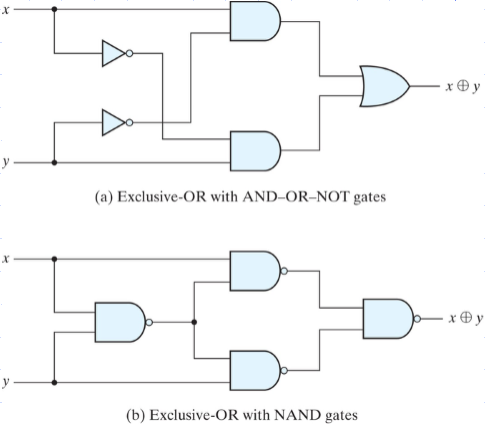 Exclusive-OR implementations
Exclusive-OR implementations
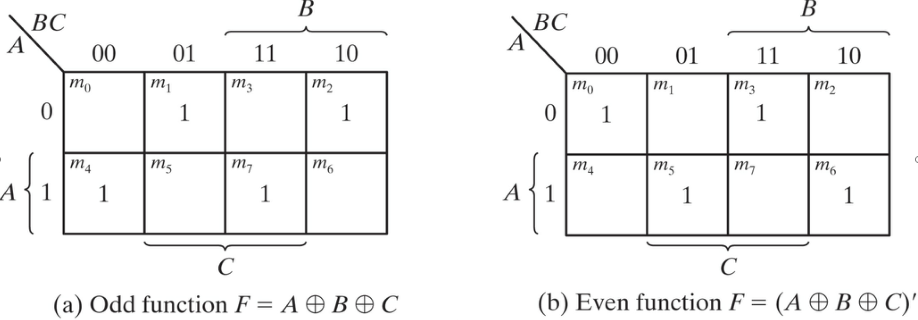 Map for a three-variable exclusive-OR function
Map for a three-variable exclusive-OR function
 Logic diagram of odd and even functions
Logic diagram of odd and even functions
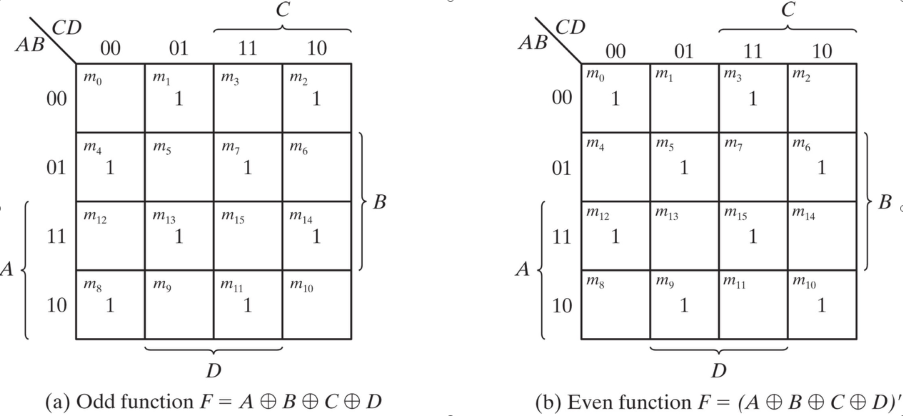 Map for a four-variable exclusive-OR function
Map for a four-variable exclusive-OR function
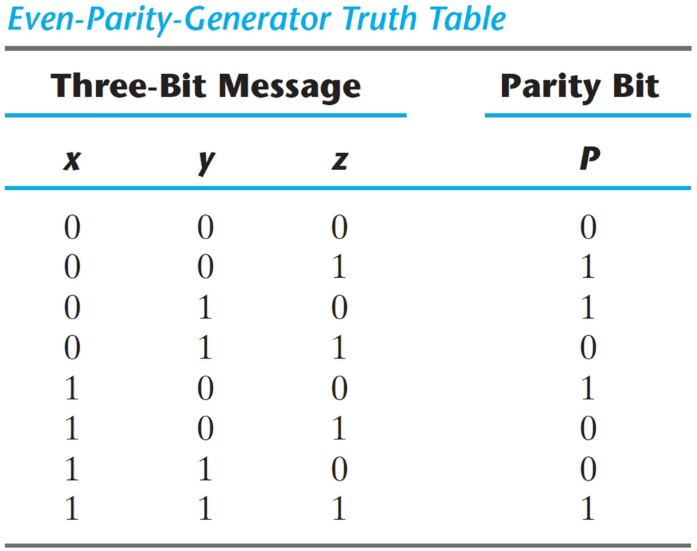
짝수 패러티 생성기 진리표
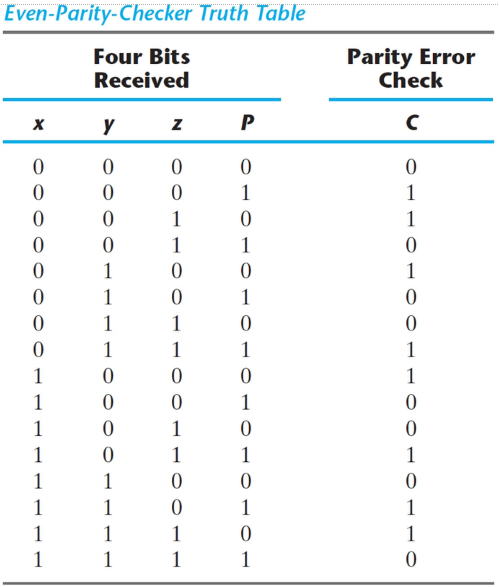
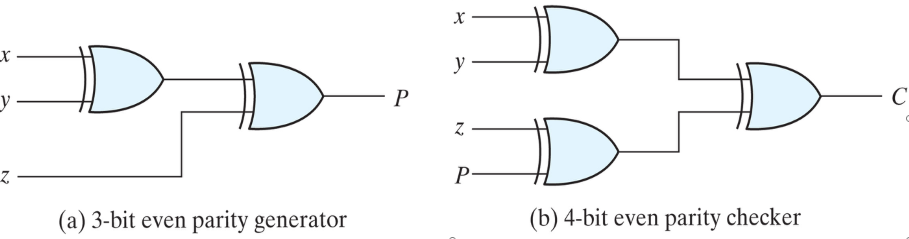 Logic diagram of a parity generator and checker
Logic diagram of a parity generator and checker
자료참조 - Digital Design 6th Morris Mano