디지털 논리 게이트와 게이트 레벨 최소화(카르노맵)
디지털 논리 게이트

다중 입력으로의 확장
2진 연산에서 교환법칙과 결합법칙이 성립하면 게이트는 다중 입력으로 확장 가능.
OR 연산, and 연산, exclusive-OR 연산
x + y = y + x
(x+y)+z=x+(y+z)= x+y+z
NAND와 NOR연산자는 결합법칙이 성립하지 않음.
(x↓y)↓z≠x↓(y↓z)
(x↓y)↓z= [(x+y)'+z]'
= (x+y)z'= xz' + yz'
x↓(y↓z)= [x+(y+z)'] '
= x'(y+z)= x'y + x'z
x↓y↓z= (x+y+z)'
x↑y↑z= (xyz)'
양논리와 음논리
2진 신호는 전이하는 동안을 제외하고는 2개의 값 중 하나를 가지며, 한 신호의 값은 1을 다른 것은 0을 나타냄.

게이트 레벨 최소화
카르노맵
네모꼴의 칸으로 구성된 도표
각 네모꼴 칸은 하나의 최소항을 나타냄
진리표를 도해한 것
Boole 함수를 축소시키기 위한 간단하고 직접적인 수단 제공
2-변수맵


3-변수맵

예시1. 다음 Boole 함수 F(x, y, z) = Σ(2, 3, 4, 5) 를 간략화하고 카르노맵으로 표현하라.
F = x'y + xy'

예시2. 다음 Boole 함수 F = x'z + x'y +xy‘z +yz 에 대하여
a) 최소항들의 합으로 나타내어라
F(x, y, z) = Σ(1, 2, 3, 5, 7)
b) 최소화된 곱의 합형태로 나타내어라
F = z + x'y

예상문제1. 다음 Boole 함수 F(x, y, z) = Σ(3, 4, 6, 7)를 간략화하고 카르노맵으로 표현하라
F = yz + xz'

예상문제2. 다음 Boole 함수 F(x, y, z) = Σ(0, 2, 4, 5, 6)를 간략화하고 카르노맵으로 표현하라
F = z’ + xy’

예상문제3. 다음 Boole 함수 A’C + A’B + AB’C + BC 를 간략화하고 카르노맵으로 표현하라
C + A’B

예상문제4. 다음 Boole 함수 F=xy + (z' + y')x' 를 간략화하고 카르노맵으로 표현하라
F = yz' + xy + x'y'
F(x, y, z) = Σ(0, 1, 2, 6, 7)
| 1 | 1 | 1 | |
| 1 | 1 |
예상문제5. 다음 Boole 함수 F=xyz + (y' + z')(x + y') 를 간략화하고 카르노맵으로 표현하라
F = x + y'
| 1 | 1 | ||
| 1 | 1 | 1 | 1 |
F(x, y, z) = Σ(0, 1, 4, 5, 6, 7)
4-변수맵

예시1. F(w, x, y, z) = Σ(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) 를 간략화 하고 카르노맵으로 표현하라
F = y'+ w'z' + xz'

예상문제1. 다음 Boole 함수 A’B’C’ + B’CD’ + A’BCD’ + AB’C’ 를 간략화 하고 카르노맵으로 표현하라
B’D’ + B’C’ + A’CD’

예상문제2. 다음 Boole 함수의 ①카르노맵을 표현하고 ②최소항의 합(Σ)과 최대항의 곱(∏)으로 표현하고 ③최소의 리터럴 수를 가지도록 표준형식(곱의 합)으로 간략화하라.
F1(w,x,y,z) = wxy(x'y +z') + (w' + xy')(x'+yz')
F1 = w'x' + xyz'
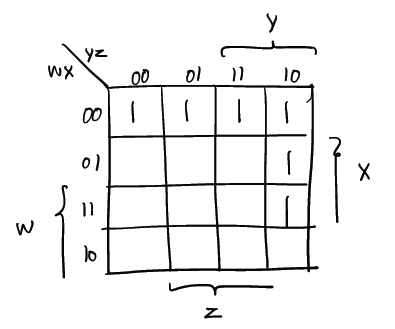
Σ(0, 1, 2, 3, 6, 14)
∏(4, 5, 7, 8, 9, 10, 11, 12, 13, 15)
F2(w,x,y,z) = wx'y(x'y +yz') + (w'x + xy')(x'+yz')
F2 = wx'y + w'xyz'

Σ(6, 10, 11)
∏(0, 1, 2, 3, 4, 5, 7, 8, 9, 12, 13, 14, 15)
F3(w,x,y,z) = (x'y +yz')wx + (x'+wyz')(w' + xy'z)
F3 = w'x' + wxyz'

Σ(0, 1, 2, 3, 14)
∏(4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15)
F4(w,x,y,z) = Σ(0, 2, 3, 5, 7, 10,11,12, 13, 15)
F4 = xz + x'y + w'x'z' + wxy'

∏(1, 4, 6, 8, 9, 14)
F5(w,x,y,z) = Σ(1, 2, 5, 7, 8, 9, 12, 13, 15)
F5 = y'z + xz + wy' + w'x'yz'

∏(0, 3, 4, 6, 10, 11, 14)
F6(w,x,y,z) =∏(1, 2, 4, 6, 7, 8, 9, 10, 11, 14, 15)
F6 = xy'z + wxy' + w'x'y'z' + w'x'yz

Σ(0, 3, 5, 12, 13)
F7(w,x,y,z) =∏(0, 3, 5, 8, 10, 11, 12, 13)
F7 = xy + x'y'z + w'xz' + w'yz'

Σ(1, 2, 4, 6, 7, 9, 14, 15)
주항 (prime implicant)
주항
- 맵 안에서 최대 개수의 인접한 네모꼴을 조합함으로써 얻을 수 있는 곱의 형태의 항
그 네모꼴을 포함하는 더 큰 네모꼴을 찾을 수 없음.
- 하나의 1이 다른 어떤 1과도 인접해 있지 않다면 그 1은 주항
- 2개의 인접한 1이 4개의 인접한 네모꼴에 포함되지 않는다면 주항
필수적 (essential)
- 하나의 최소항을 나타내는 네모꼴이 오직 하나의 주항에만 포함된다면 그 주항은 필수적임.

필수 주항 (BD, B'D') 주항 (CD, B'C, AD, AB')
F=BD+B'D'+CD+AD
=BD+B'D'+CD+AB'
=BD+B'D'+B'C+AD
=BD+B'D'+B'C +AB'

5-변수맵

예시 ) 다음 Boole 함수를 간략화하라. F(A,B,C,D,E)=Σ(0,2,4,6,9,13,21,23,25,29,31)
F = A'B'E' + BD'E + ACE

합의 곱 간략화
다음의 Boole함수를 간략화하라. F(A, B, C, D) = Σ(0, 1, 2, 5, 8, 9, 10)

곱의 합
F = B'D' + B‘C' +A'C'D
합의 곱
F' = AB + CD + BD'
F = (A' +B')(C' +D')(B' +D)
Don’t-care 조건
함수에서 규정되지 않은 최소항
- 어떤 값을 취하여도 상관 없음.
- 0 이나 1 어느 값이든 가질 수 있음.
- Boole 함수의 표현을 더욱 간략화하는 데 사용될 수 있음.
예시 ) Don`t care 조건, d(w, x, y, z) = Σ(0, 2, 5) 을 갖는 다음 Boole 함수를 간략화하라 F(w, x, y, z) = Σ(1,3,7,11,15)

>> F(w, x, y, z) = yz + w'x' = Σ(0, 1, 2, 3, 7, 11, 15)
>> F(w, x, y, z) = yz + w'z = Σ(1, 3, 5, 7, 11, 15)
예상 문제1 F(A,B,C,D,E)=Σ(2,4,6,9,21,23,29,31)
예상 문제2 F(A,B,C,D,E)=Σ(0,2,9,13,21,23,25)
예상 문제3 F(A,B,C,D,E) = ∏(0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 30, 31)
예상 문제4 Don`t care 조건, d(A,B,C,D) = Σ(13, 14) 을 갖는 다음 Boole 함수를 간략화라.
F(A,B,C,D) = Σ(0,1,2, 3, 7,11,12,15)
예상 문제5 Don`t care 조건, d(A,B,C,D) = Σ(11, 15) 을 갖는 다음 Boole 함수를 간략화하라.
F(A,B,C,D) = Σ(1,3,7,8,9,10,12,14)
자료참조 - Digital Design 6th Morris Mano
'컴퓨터공학 💻 > 디지털 시스템 회로 설계' 카테고리의 다른 글
| [디지털 시스템 회로 설계] 디코더, 인코더, 멀티플렉서, 디멀티플렉서 (0) | 2021.10.27 |
|---|---|
| [디지털 시스템 회로 설계] 논리 회로 - 조합 회로 (0) | 2021.10.18 |
| [디지털 시스템 회로 설계] NAND 게이트, NOR 게이트 구현, Exclusive-OR 함수 (0) | 2021.10.16 |
| [디지털 시스템 회로 설계] 부울 대수와 논리게이트 (0) | 2021.09.17 |
| [디지털 시스템 회로 설계] 디지털 시스템과 이진 시스템 (0) | 2021.09.08 |




