[디지털 시스템 회로 설계] 디지털 시스템과 이진 시스템

[디지털 시스템 회로 설계] 디지털 시스템과 이진 시스템

디지털 시스템 (Digital System)

이진 형태로 나타나는 정보의 이산적 요소(discrete element)를 처리하는 시스템이다.

> 정보의 이산적 요소는 신호 (signal)라고 불리는 물리적 양에 의해 결정된다.

> 신호: 전압, 전류 같은 전기적 신호

디지털 시스템은 디지털 모듈을 서로 연결하여 구성한다.

> 여러 종류의 디지털 모듈의 동작을 이해하기 위해서는 디지털 논리 회로에 대한 지식이 필요하다.

 

기수 변환

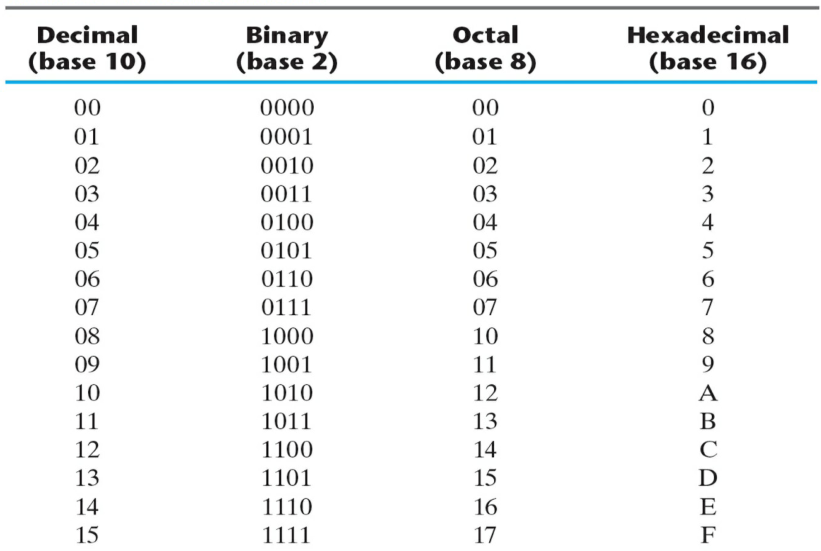<진수값 표>

2진수 -> 10진수

11010.11(2)

1×2^4 + 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0 + 1×2^-1 + 1×2^-2 

= 26.75(10)

 

10진수 -> 2진수

41

41 / 2 .. 1

20 / 2 .. 0

10 / 2 .. 0

5 / 2 .. 1

2 / 2 .. 0

1 / 2 .. 1

= 101001

 

153

153/2 .. 1

76/2 .. 0

38/2 .. 0

19/2 .. 1

9/2 .. 1

4/2 .. 0

2/2 .. 0

1/2 .. 1

= 10011001

 

0.6875

0.6875 * 2 = 1 + 0.3750

0.3750 * 2 = 0 + 0.7500

0.7500 * 2 = 1 + 0.5000

0.5000 * 2 = 1 + 0.0000

= 0.1011

 

10진수 -> 8진수

153

153 / 8 .. 1

19 / 8 .. 3

2 / 8 .. 2

= 231

 

2진수 -> 8진수

10 110 001 101 011.111 100 000 110

=26153.7406

 

2진수 -> 16진수

10 1100 0110 1011 . 1111 0000 0110

=2C6B.F06 

 

 

보수 (complement)

컴퓨터에서 뺄셈을 간단히 하거나 논리연산을 하는데 사용된다.

기보수 : r의 보수

감소된 기보수 : (r-1)의 보수

 

감소된 기보수

기수가 r, 자리수가 n인 숫자 N이 존재할 때 N에 대한 (r-1)의 보수 : ((r^n)-1)-N

예시 1. N에 대한 9의 보수는 ((10^n)-1)-N 이다.

> 546700에 대한 9의 보수는 999999 - 546700 = 453299

> 012398에 대한 9의 보수는 999999 - 012398 = 987601 

예시 2. 2진수에 대해, r=2, r-1=1 일 때 N에 대한 1의 보수는 ((2^n)-1)-N 

> 1011000에 대한 1의 보수는 0100111

> 0101101에 대한 1의 보수는 1010010 

※ 2진수에 N에 대해 1의 보수는 !N과 같음.

 

기보수

n 자리의 숫자 N에 대한 r의 보수는 N≠0 일 때 : r^n - N. N=0 일 때 : 0

r^n - N = [(r^n - 1) - N] + 1

-> r의 보수는 (r-1)의 보수에 1을 더하면 구해짐. 

예시

> 012398에 대한 10의 보수는 987602

> 246700에 대한 10의 보수는 753300 

> 1101100에 대한 2의 보수는 0010100

> 0110111에 대한 2의 보수는 1001001 

※ 2진수 N에 대해 2의 보수는 !N +1과 같음

 

 

 

부호화된 2진수

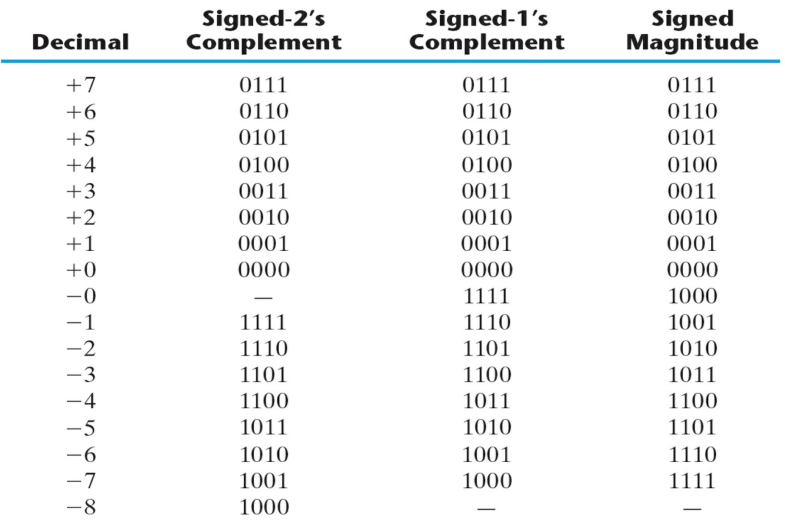
2진수의 부호를 표시할 때 가장 앞의 1비트를 양수는 0, 음수는 1로 처리한다.

예시

8비트의 2진수로 표현된 9

> +9 = 0000 1001

> -9 = 1000 1001 (부호 크기 방식)

> -9 = 1111 0110 (부호화된 1의 보수)

> -9 = 1111 0111 (부호화된 2의 보수)

 

산술 덧셈

부호-크기 방식에서 두 수의 덧셈은 일반적인 연산방법으로 계산한다.

부호-보수 방식은 덧셈만 가능.

> 부호 비트를 더할 때 생기는 올림수는 무시한다.

> 덧셈을 한 후 합이 음수라면 그 합 또한 2의 보수 형태가 된다.

> 오버플로우(overflow): n 비트 수를 더할 때 n+1 비트의 결과가 얻어지는 현상.

 

산술 뺄셈

피감수의 부호를 바꾸어서 뺄셈을 덧셈의 형태로 바꾼다.

감수(부호 비트를 포함해서)의 2의 보수를 취한 다음, 그것을 피감수에 더한다.

(±A)-(+B) = (±A)+(-B)

(±A)-(-B) = (±A)+(+B)  

덧셈과 뺄셈에 공통된 하드웨어 회로 사용 가능하다.

 

기본 예제

(1)     3

   +(-32)

(2)   -64

   +(-64)

(3)   -100

    +  100

(4)   -100

   +(-100)

(5)    100

    + 100

  (1) -29
  0000 0011
  1110 0000
  ---------
  1110 0010
  
  (2) -128
  1100 0000
  1100 0000
  ---------
  1000 0000
  
  (3) 0
  1001 1100
  0110 0100
  ---------
  0000 0000
  
  (4) -200, overflow 발생!
  1001 1100
  1001 1100
  ---------
  0011 1000
  
  (5) 200, overflow 발생!
  0110 0100
  0110 0100
  ---------
  1100 1000

 

 

2진 코드 - BCD 코드

한자리 숫자를 표현하기 위한 4비트 코드

예시

> 185(10) = 0001 1000 0101(BCD) = 10111001(2)

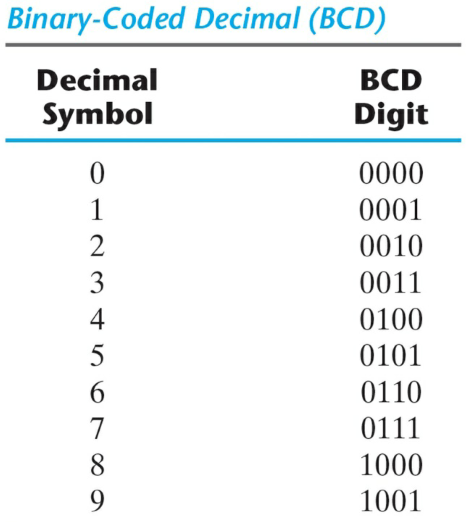
BCD 코드 덧셈

BCD 코드로 이루어진 2진수의 합이 1010보다 크거나 같으면 0110을 더해서 올바른 BCD합을 만든다. 

예시

 4    0100    4    0100    8    1000
+5   +0101   +8   +1000   +9   +1001
------------------------------------
 9    1001   12    1100   17   10001
                  +0110        +0110
                  ------------------
                  10010        10111

올림수가 발생하면 올림수를 포함하여 더한다.

예시

# 347 + 658 = 1005
    0011	    0100	    0111
    0110	    0101	    1000
--------------------------------
    1010	    1010	    1111
 +  0110	 +  0110	 +  0110
--------------------------------
 1  0000	 1  0000	 1  0101
 1  0000	    0000	    0101 (결과)

 

2진 코드 - 다른 형식의 10진 코드

2421은 각 비트의 값이 2, 4, 2, 1임을 의미한다.

Excess-3은 Digit Number + 3의 값을 의미한다.

8, 4, -2, -1은 각 비트의 값이 8, 4, -2, -1임을 의미한다.

이외에도 여러가지 형식이 존재한다

 

2진 코드 - 그레이 코드

한 숫자에서 다음 숫자로 변할 때 코드의 단 한 비트만 변하는 코드. 아날로그 형태를 디지털 형태로 바꿀 때 편리할 수 있다.

회전 축이 회전할 때 회전축의 위치가 연속적으로 변화하는 것 등에 적용하며 변이 과정에서 에매함이나 오류가 발생할 확률이 적다.

 

2진 코드 - 아스키 코드 (ASCII Character Code)

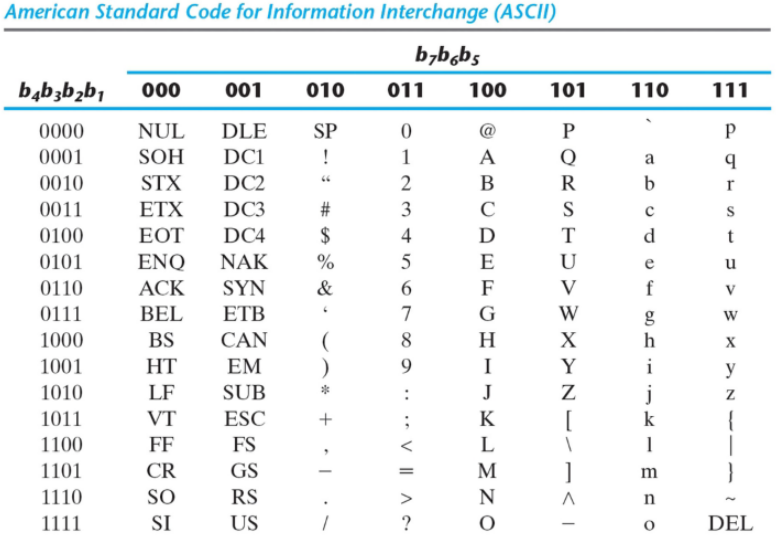
오류 검출 코드 - 패러티 비트 (parity bit)

데이터를 통신하거나 처리하는 과정에서 에러를 검출하기 위해 ASCII 문자에 한 비트를 더해서 만든 비트.

	짝수 패러티	홀수 패러티
ASCII A = 1000001	01000001	11000001
ASCII T = 1010100	11010100	01010100

1의 개수를 기준으로 오류를 판단한다. 짝수 패러티에서는 1의 개수를 짝수가 되도록 더하며 홀수 패러티에서는 반대로 1의 개수가 홀수가 되도록 비트를 더한다.

 

2진 기억장치와 레지스터

2진 셀 (binary cell): 2개의 안정된 상태를 가진다.

레지스터 : 2진 셀을 모아 놓은 것.

레지스터 전이 (register transfer)

 

2진 논리 (Binary Logic)

2개의 이산적인 값을 갖는 변수와 논리연산을 다룬다.

 

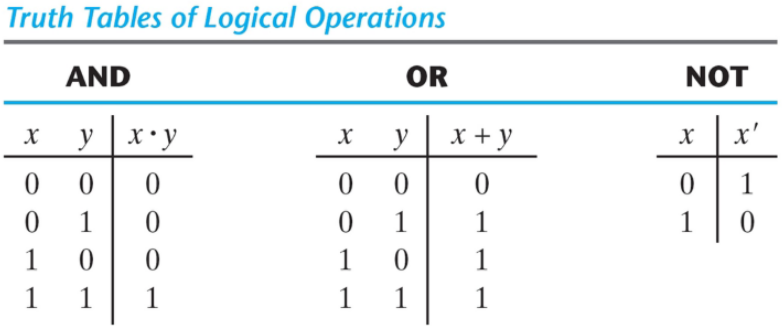
논리 게이트

하나 이상의 입력 신호를 받아 출력신호를 만드는 전자회로.

디지털 시스템에는 전압이나 전류를 이용한 전기적인 신호가 두 가지 값으로 존재한다.

 

 

 

자료참조 - Digital Design 6th Morris Mano