[알고리즘] 정렬 알고리즘
- -
선택 정렬
수행시간
최악: (n-1)+(n-2)+···+2+1 = Θ(n2)
평균: (n-1)+(n-2)+···+2+1 = Θ(n2)
• 각 루프마다
– 최대 원소를 찾는다
– 최대 원소와 맨 오른쪽 원소를 교환한다
– 맨 오른쪽 원소를 제외한다
• 하나의 원소만 남을 때까지 위의 루프를 반복
# 일반
selectionSort(A[], n) { # A[1 ... n]을 정렬한다
for last <- n downto 2 { # ①
k <- theLargest(A, last); # ②
A[k] <-> A[last]; # ③ A[k]와 A[last]의 값을 교환
}
}
theLargest(A[], last) {
largest <- 1;
for i <- 2 to last
if (A[i] > A[largest]) then largest <- i;
return largest;
}
# 재귀형
selectionSort_req(A[], n) { # A[1 ... n]을 정렬한다
if (n == 1) return A[];
max = -INT_MAX;
for i <- 1 to n {
if (max < A[i]) {
max = A[i];
k = i;
}
}
temp = A[n];
A[n] = A[k];
A[k] = temp;
return selectionSort_req(A, n-1);
}
①의 for 루프는 n-1번 반복
②에서 가장 큰 수를 찾기 위한 비교횟수: n-1, n-2, …, 2, 1
③의 교환은 상수 시간 작업
버블 정렬
수행 시간
최악: (n-1)+(n-2)+···+2+1 = Θ(n^2)
평균: (n-1)+(n-2)+···+2+1 = Θ(n^2)
# 일반
bubbleSort(A[], n) { # A[1 ... n]을 정렬한다
for last <- n downto 2 # ①
for i <- 1 to last-1 # ②
if(A[i] > A[i+1]) then A[i] <-> A[i+1] # # ③ 원소 교환
}
# 재귀형
bubbleSort_rcn(A[], n) { # A[1 ... n]을 정렬한다, n >= 1
if (n > 1) {
for i <- 1 to n-1
if(A[i] > A[i+1]) then A[i] <-> A[i+1] # 원소 교환
bubbleSort_rcn(A, n-1)
}
}①의 for 루프는 n-1번 반복
②의 for 루프는 각각 n-1, n-2, …, 2, 1번 반복
③은 상수 시간 작업
• 선택정렬과 버블정렬은 아직 정렬되지 않은 배열의 크기를 하나씩 줄이는 정렬
삽입 정렬
수행 시간
최악: 1+2+···+(n-2)+(n-1) = Θ(n^2)
평균: ½ (1+2+···+(n-2)+(n-1)) = Θ(n^2)
최선: 1+1+···+1+1 = n - 1 = Θ(n)
# 일반
insertionSort(A[], n) { # A[1 ... n]을 정렬한다
for i <- 2 to n { # ①
loc <- i-1; # ②
newItem <- A[i] # 이 지점에서 A[1 ... i-1]은 이미 정렬되어 있다
while (loc >= 1 && newItem < A[loc]) { # 최대 i-1번 반복
A[loc+1] <- A[loc]
loc--
}
A[loc+1] <- newItem
}
}
# 재귀형
insertionSort_rcn(A[], n) { # A[1 ... n]을 정렬한다, n >= 1
if (n <= 1) return;
insertionSort(A, n-1);
last = A[n-1];
i = n-2;
while (i >= 0 && A[i] > last) {
A[i+1] = A[i];
i--;
}
A[i+1] = last;
}①의 for 루프는 n-1번 반복
②의 삽입은 최악의 경우 i-1회 비교
• 배열 A[1]만 놓고 보면 정렬되어 있음
• 배열 A[1 … k]까지 정렬되어 있다면 행의 삽입에 의해 A[1 … k+1]까지 정렬된다 (귀납적 성질)
• 배열이 대부분 정렬된 채로 적용할 때 매력적인 알고리즘
• 이미 정렬된 배열의 크기를 하나씩 늘리는 정렬
병합정렬
점화식(평균) : T(n) = 2T(n/2) + cn
시간복잡도 : Θ(nlogn)
mergeSort(A[], p, r) {
if (p < r) then {
q <- floor(p+r/2); # p, r의 중간지점 계산
mergeSort(A, p, q); # 전반부 정렬
mergeSort(A, q+1, r); # 후반부 정렬
merge(A, p, q, r); # 병합
}
}
merge(A[], p, q, r) {
# A[p ... q]와 A[q+1 ... r]을 병합하여 A[p ... r]을 정렬된 상태로 만든다
# A[p ... q]와 A[q+1 ... r]은 이미 정렬되어 있다
i <- p; j <- q+1; t <- 1;
while (i <= q && j <= r) {
if (A[i] <= A[j])
tmp[t++] <- A[i++];
else tmp[t++] <- A[j++];
}
while (i <= q) # 왼쪽 부분 배열이 남은 경우
tmp[t++] <- A[i++];
while (j <= r) # 오른쪽 부분 배열이 남은 경우
tmp[t++] <- A[j++];
i <- p; t <- 1;
while (i <= r) # 결과를 A[p ... r]에 저장
A[i++] <- tmp[t++];
}예제 다음 수들을 merge sort하는 과정을 나타내시오 ( 5 4 7 2 )
(1) mergeSort(A[],p,r)이 불리는 순서를 적고 mergeSort(A[],p,r)가 마쳐질 때마다 A[]의 상태를 보인다.
(2) mergeSort의 출력 횟수를 구한다.
퀵 정렬
점화식(최악) : T(n) = T(n-1) + n (이미 정렬이되어있는경우)
점화식(최선, 평균) : T(n) = 2T(n/2) + n
시간복잡도 : Θ(nlogn)
퀵 정렬의 성질
• 분할이 항상 반반씩 균등할 경우 가장 이상적
• for 루프가 한번 돌때마다 3구역이 한칸씩 줄어든다
• for 루프가 한번 돌때마다 1구역 또는 2구역 중 하나가 한칸 늘어난다
• 2구역이 늘어날 때는 j만 증가한다. for 루프가 한번 돌때마다 j는 1 증가하므로 2구역을 늘리기 위해서는 아무일도 할 필요가 없다.
• 1구역이 늘어날 때는 i와 j가 동시에 증가한다.
quickSort(A[], p, r) # A[p ... r]을 정렬한다
{
if (p < r) then {
q = partition(A, p, r); # 분할
quickSort(A, p, q-1); # 왼쪽 부분 배열 정렬
quickSort(A, q+1, r); # 오른쪽 부분 배열 정렬
}
}
partition(A[], p, r)
{
# 배열 A[p ... r]의 원소들을 A[r]을 기준으로 양쪽으로 재배치
x <- A[r]; # 기준 원소
i <- p-1; # i는 1구역의 끝지점
for j <- p to r-1 # j는 3구역의 시작지점
if (A[j] <= x) then A[++i] <-> A[j]; # i값 증가 후 A[i] <-> A[j]
A[i+1] <-> A[r]; # 기준 원소와 2구역 첫 원소 교환
return i+1; # A[r]이 자리한 위치를 리턴;
}
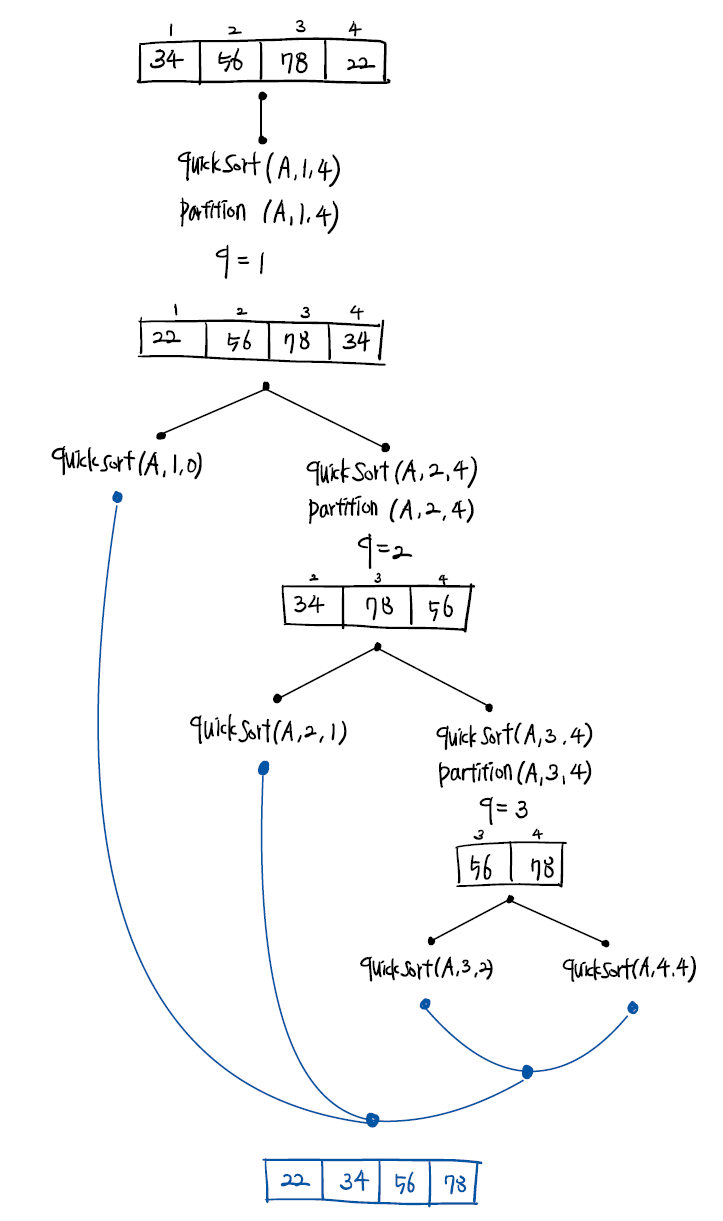
예제 다음 수들을 quick sort하는 과정을 나타내시오.
quickSort(A[],p,r)이 불리는 순서를 적고 partition(A[],p,r)가 마쳐질 때마다 A[]와 q의 상태를 보이면 된다. 추가적으로 quickSort()의 총 호출 수를 기록하시오.
34 56 78 22
총 호출 수 : 7
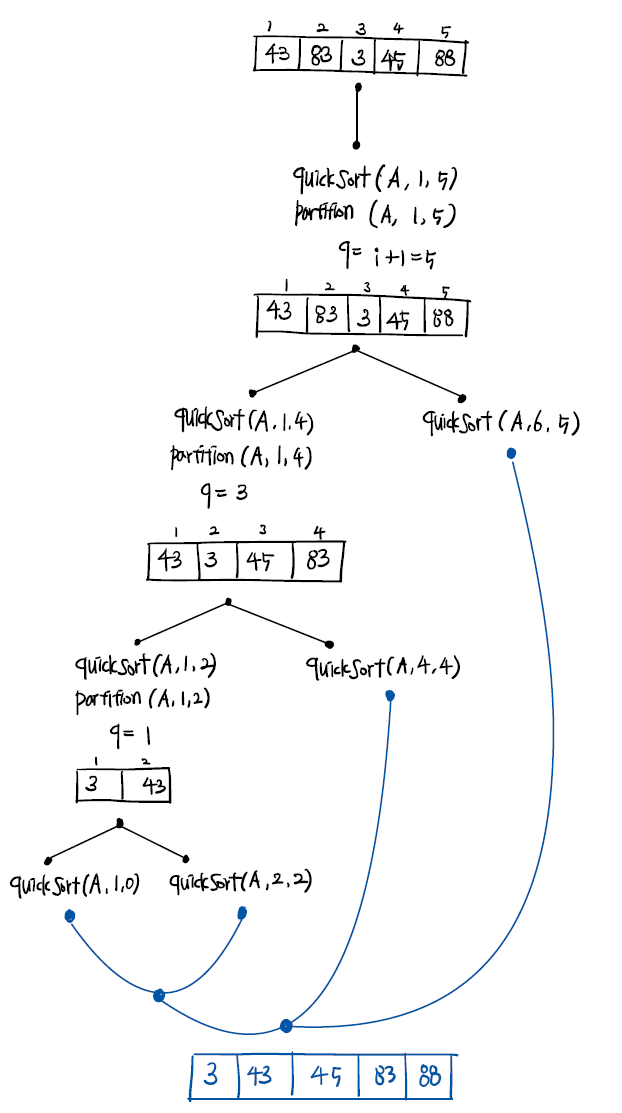
43 83 3 45 88
총 호출 수 : 7
힙 정렬
힙(Heap)
Complete binary tree로서 다음의 성질을 만족한다
- 각 노드의 값은 자신의 children의 값보다 크지 않다 (최소 힙)
- 노드가 1개이거나 빈 트리도 힙이다
힙정렬
주어진 배열을 힙으로 만든 다음, 차례로 하나씩 힙에서 제거함으로써 정렬한다
시간복잡도
Average Case : heapify(logn) * buildHeap(n) = O(nlogn)
Worst Case : O(nlogn)
buildHeap(A[], n) { # A[1...n]을 힙으로 만든다.
for i <- [n/2] downto 1
heapify(A, i, n)
}
heapify(A[], k, n) {
# A[k]를 루트로 하는 트리를 힙 성질을 만족하도록 조정한다.
# A[k]의 두 자식을 루트로 하는 서브트리는 힙 성질을 만족하고 있다.
# n은 최대 인덱스(전체 배열의 크기)
left <- 2k; right <- 2k+1; # 작은 자식(smaller) 고르기.
if (right <= n) then { # k가 두 자식을 가지는 경우
if (A[left] < A[right]) then smaller <- left;
else smaller <- right;
}
else if (left <= n) then smaller <- left; # k의 왼쪽 자식만 있는 경우
else return; # 종료조건1 (A[k]가 리프 노드임)
# 재귀적 조정
if (A[smaller] < A[k]) then { # 종료조건2 (자식노드가 부모보다 크면 종료)
A[k] <-> A[smaller];
heapify(A, smaller, n);
}
}
heapSort(A[], n) { # A[1...n]을 정렬한다
buildHeap(A, n); # 힙 만들기
for i <- n downto 2 {
A[1] <-> A[i]; # 원소 교환
heapify(A, 1, i-1);
}
}예제1 ) 1 30 2 7 6 5 4 13 12 11 10 9 8
(1) 배열 A가 위와 같으며 index 1부터 값이 들어 있다. buildHeap(A, 13)을 호출했을 때 for문을 도는 횟수와 heapify()를 총 몇번 호출하는가?
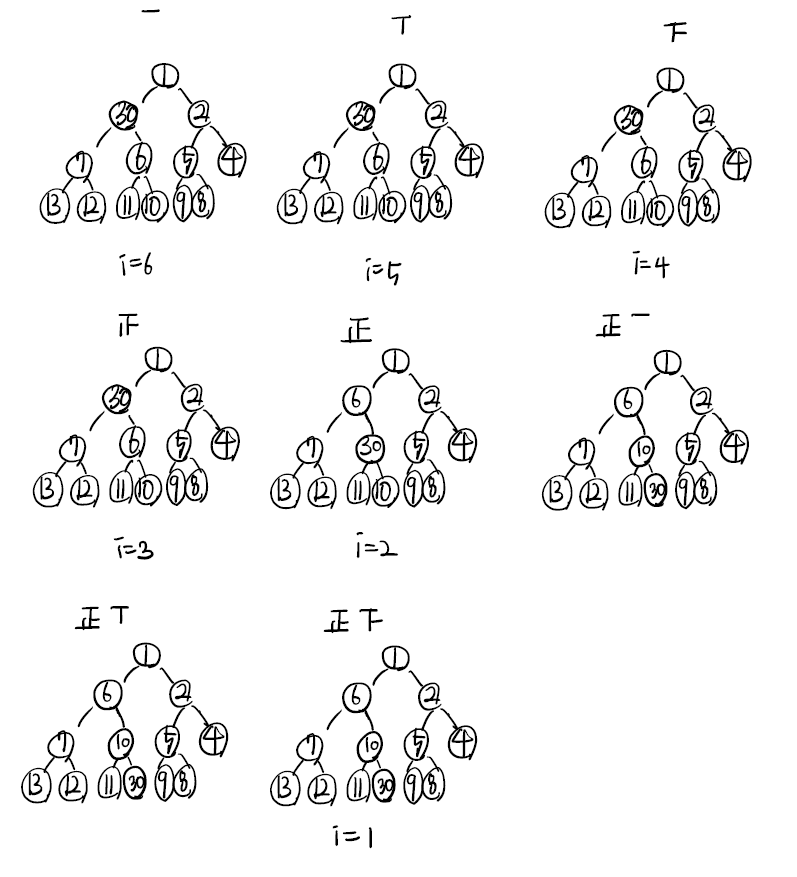
(2) heapify(2, 9)을 적용한 후 배열 A의 상태를 나타내라.
(3) 알고리즘 heapify()의 시간 복잡도는 얼마인가? 그 이유를 설명하시오.
- 최악의 경우를 고려, if문내에서 트리의 높이만큼 재귀호출되어 log2(n) + c = logn만큼 수행한다.
두수 비교정렬 하한 Ω(nlogn)
• 잎노드수가 2k인 완전이진트리의 (내부)깊이는 k이다.
• 잎노드수가 N인 이진트리의 깊이는 적어도 log2N이다.
• 잎노드수가 n!인 이진트리의 깊이는 적어도 log2 n!이다.
• log2 n! > log ( n/2 ) n/2 = Ω (n log n)
계수 정렬 (Counting Sort)
수행시간 : Θ(n)
k = O(n)이면 총 시간 Θ(n)
k > O(n)이면 총 시간 Θ(k) : k가 nlogn 이상인 경우 계수 정렬을 쓰는 이유가 없음
countingSort(A[], B[], n) {
# A[1 ... n]: 입력 배열
# B[1 ... n]: 배열 A[]를 정렬한 결과 배열
for i <- 1 to k
C[i] <- 0;
for j <- 1 to n
C[A[j]]++; # 이 시점에서 C[i]: 값이 i인 원소의 총 수
for i <- 2 to k
C[i] <- C[i] + C[i-1]; # 이 시점에서 C[i]: i보다 작거나 같은 원소의 총 수
for j <- n downto 1 {
B[C[A[j]]] <- A[j];
C[A[j]]--;
}
}
기수 정렬 (Radix Sort)
radixSort(A[ ], n, k) {
# 원소들이 각각 최대 k 자리수인 A[1…n]을 정렬한다
# 가장 낮은 자리수를 1번째 자리수라 한다
for i <- 1 to k
i번째 자릿수에 대해 A[1 ... n]을 안정성을 유지하면서 정렬한다;
}안정성 정렬 (Stable sort) : 같은 값을 가진 원소들은 정렬 후에도 원래의 순서가 유지되는 성질을 가진 정렬을 일컫는다.
'컴퓨터공학 💻 > 알고리즘 분석' 카테고리의 다른 글
| [알고리즘] 다진 검색 트리 (B-tree) (0) | 2021.11.22 |
|---|---|
| [알고리즘] 이진 검색트리와 레드블랙트리 (0) | 2021.11.06 |
| [알고리즘] 점화식과 점근적 복잡도 분석 (0) | 2021.09.27 |
| [알고리즘] 알고리즘의 점근적 분석 : 상한, 하한, 동등 (0) | 2021.09.19 |
| [알고리즘] 알고리즘 시간 복잡도 분석과 수행시간을 좌우하는 기준 (0) | 2021.09.06 |
소중한 공감 감사합니다

