[알고리즘] 이진 검색트리와 레드블랙트리

검색 알고리즘

기타 개념

> 레코드record

– 개체에 대해 수집된 모든 정보를 포함하고 있는 저장 단위

– e.g., 사람의 레코드

주민번호, 이름, 집주소, 집 전화번호, 직장 전화번호, 휴대폰 번호, 최종 학력, 연소득, 가족 상황 등의 정보 포함

> 필드field 

– 레코드에서 각각의 정보를 나타내는 부분

– e.g., 위 사람의 레코드에서 각각의 정보를 나타내는 부분

> 검색키search key 또는 키key

– 다른 레코드와 중복되지 않도록 각 레코드를 대표할 수 있는 필드

– 키는 하나의 필드로 이루어질 수도 있고, 두 개 이상의 필드로 이루어질 수도 있다

> 검색트리search tree

– 각 노드가 규칙에 맞도록 하나씩의 키를 갖고 있다

– 이를 통해 해당 레코드가 저장된 위치를 알 수 있다

 

이진 검색트리

• 각 노드는 키값을 하나씩 갖는다. 각 노드의 키값은 모두 달라야 한다.

• 최상위 레벨에 루트 노드가 있고, 각 노드는 최대 두 개의 자식을 갖는다.

• 임의의 노드의 키값은 자신의 왼쪽 자식 노드의 키값보다 크고, 오른쪽 자식의 키값보다 작다.

treeSearch(t, x) {
    # t: 트리의 루트 노드
    # x: 검색하고자 하는 키 
	if (t=NIL(공백) or key[t]=x) then return t;                      
	if (x < key[t]) 
		then return treeSearch(left[t], x); 
		else return treeSearch(right[t], x);       
}

시간 복잡도 : 트리의 깊이

최선 O(logn), 최악 O(n)

 

[예제] 다음 이진트리에서 treeSearch(2, 25), treeSearch(1, 70)의 리턴 값과 호출 수는?

treeSearch(2, 25) = 9, 호출 수 = 3

treeSearch(1, 70) = NIL, 호출 수 = 3

 

이진 검색트리에서의 삽입

treeInsert(t, x) {
    # t: 트리의 루트 노드
    # x: 삽입하고자 하는 키
    # 작업 완료 후 루트 노드의 포인터를 리턴한다
	if (t=NIL) then { 
		key[r] ← x;  left[r] ← NIL;  right[r] ← NIL;    ▷ r : 새 노드 
		return r ;         
	} 
	if (x < key[t]) 
		then {left[t] ← treeInsert(left[t], x); return t;} 
		else {right[t] ← treeInsert(right[t], x); return t;}
}

시간 복잡도 : 트리의 깊이

최선 Θ(logn) 점화식 T(n) = T(n/2) + 1

최악 O(n) 점화식 T(n) = T(n-1) + 1

 

[예제] 다음 이진트리에서 treeInsert(1, 25)의 리턴 값과 treeInsert의 호출 수는?

treeInsert(1, 25) = 1, 호출 수 = 3

[예제] 다음 이진트리에서 treeInsert(1, 23)의 리턴 값과 treeInsert의 호출 수, 호출 순서는?

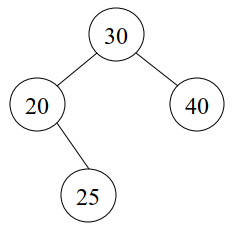
treeInsert(1, 23) = 1, 호출 수 = 4

호출 순서 : treeInsert(1,23) -> treeInsert(2,23) -> treeInsert(5,23) -> treeInsert(NIL,23)

 

이진 검색트리에서의 삭제

3가지 경우에 따라 다르게 처리한다

– Case 1 : r이 리프 노드인 경우

– Case 2 : r의 자식 노드가 하나인 경우

– Case 3 : r의 자식 노드가 두 개인 경우

treeDelete(t, r, p) { 
	if (r = t) then root ← deleteNode(t);     	# r이 루트 노드인 경우     
	else if (r = left[p]) 			▷ r이 루트가 아닌 경우
		then left[p] ← deleteNode(r); 		# r이 p의 왼쪽 자식 
		else right[p] ← deleteNode(r); 		# r이 p의 오른쪽 자식 
} 
deleteNode(r) {        
        if (left[r] = right[r] = NIL) then return NIL;	# Case 1 
        else if (left[r] = NIL and right[r] ≠ NIL) then return right[r]; # Case 2-1 
        else if (left[r] ≠ NIL and right[r] = NIL) then return left[r];	 # Case 2-2 
        else {	  # Case 3 
            s ← right[r]; 
            while (left[s] ≠ NIL)
                    {parent ← s;  s ← left[s];}
            key[r] ← key[s]; 
            if (s = right[r]) then right[r] ← right[s];
                   else left[parent] ← right[s];
            return r; 
        } 
}

treeDelete()의 시간복잡도: 상수 이내

deleteNode()의 시간복잡도 : 트리의 깊이

평균 O(logn) 

최악 O(n)

 

[예제] 물음에 답하시오.

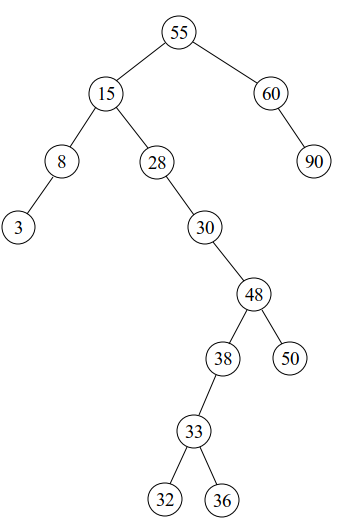
1)위 이진검색트리에서 deleteNode(30), deleteNode(48)을 수행했을 때의 return값은?

[풀이] 30의 오른쪽 자식 트리(48)의 위치를 반환한다.

[풀이] 48의 직후 원소(50)를 48의 위치로 옮기고 50의 위치를 반환한다.

 

2.

[예제] 다음 이진검색트리에서 18을 제거했을 때의 

 

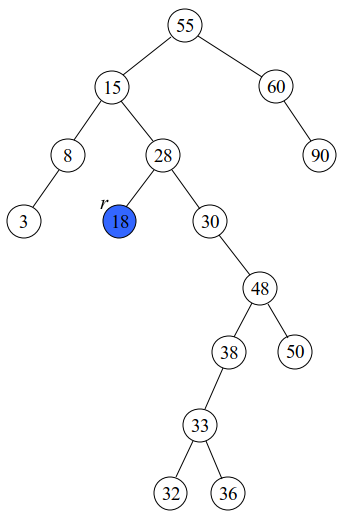
레드블랙트리

이진검색트리의 모든 노드에 블랙 또는 레드의 색을 칠하되 다음의 레드블랙특성을 만족해야 한다

① 루트는 블랙이다

② 모든 리프는 블랙이다

③ 노드가 레드이면 그 노드의 자식은 반드시 블랙이다

④ 루트 노드에서 임의의 리프 노드에 이르는 경로에서 만나는 블랙 노드의 수는 모두 같다

※ 여기서 리프 노드는 일반적인 의미의 리프 노드와 다르다. 모든 NIL 포인터가 NIL이라는 리프 노드를 가리킨다고 가정한다.

 

※ 참고 : 레드블랙트리의 검색 알고리즘은 이진 검색알고리즘의 방식을 따른다. 따라서 시간복잡도 역시 트리의 높이(깊이)이며 평균 O(logn), 최악 O(n)이다.

 

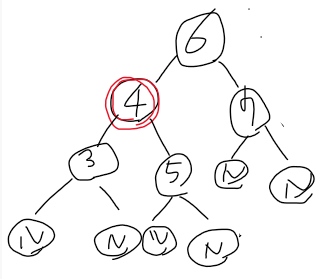
[예시] 레드블랙트리의 예시

레드블랙트리의 높이 증명

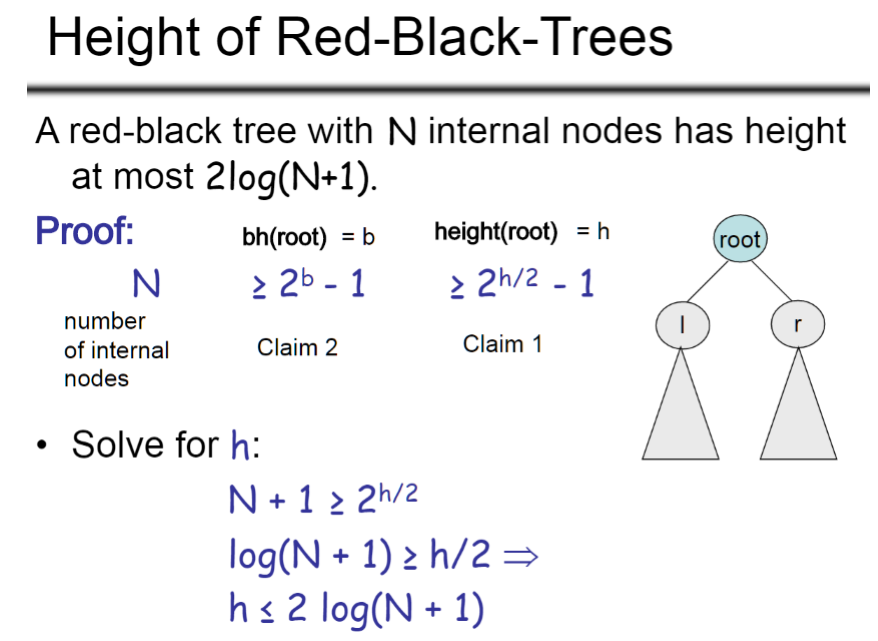
Claim 1( 2^b - 1 >= 2^(h/2) - 1 ) 가 성립하는 이유?

proof 1) 위 식은 b >= h/2를 증명하라는 의미와 같다. 만약 레드블랙트리의 모든 노드가 블랙이라면 b = h이므로 식이 성립한다.

proof 2) 레드 노드의 자식은 반드시 블랙이다. 레드 노드의 개수는 기껏해야 노드의 절반보다 많을 수는 없다. 따라서 블랙 노드의 수가 전체 노드 수의 절반보다 많을 수밖에 없다. 따라서 위 식은 성립한다.

 

Claim 2( N >= 2^b - 1 ) 가 성립하는 이유? 수학적 귀납법

N_sub = N_sub1 + N_sub2 + 1

        >= (2^k - 1) + (2^k - 1) + 1

        >= (2^k - 1)

따라서 b가 k+1인 경우 N은 다음과 같은 수식으로 정리된다.

N >= (2^k - 1) + (2^k - 1) + 1 = 2^(k+1) - 1

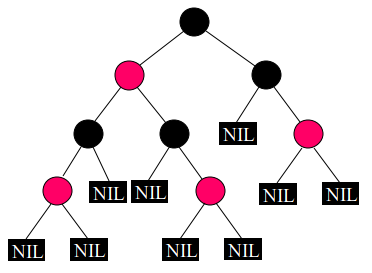
[예시] 다음 레드블랙트리의 h와 b는?

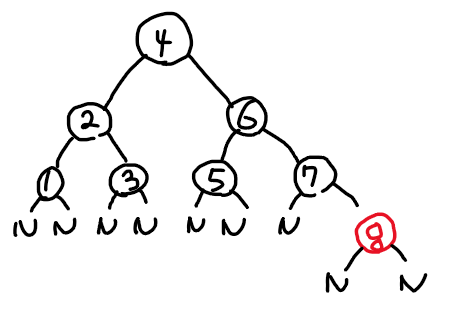
h = 4, b = 3

레드블랙트리의 삽입

이진검색트리에서의 삽입과 같다. 다만 삽입 후 삽입된 노드를 레드로 칠한다. (이 노드를 x라 하자)

만일 x의 부모 노드 p의 색상이

– 블랙이면 아무 문제 없다.

– 레드이면 레드블랙특성 ③이 깨진다.

그러므로 p가 레드인 경우만 고려하면 된다

p2와 x의 형제 노드는 반드시 블랙이다

s의 색상에 따라 두 가지로 나눈다

– Case 1: s가 레드

– Case 2: s가 블랙

    Case 2-1: x가 p의 오른쪽 자식 (= x와 p와 p2가 꺾인선상에 있는 경우)

    Case 2-2: x가 p의 왼쪽 자식 (= x와 p와 p2가 일직선상에 있는 경우)

[Case 1] s가 레드

p와 s를 레드에서 블랙으로 바꾸고 p2를 블랙에서 레드로 바꾼다.

- p2가 루트이면 다시 블랙으로 바꾸고 종료.

- p2가 루트가 아니면 p2가 부모 색상을 확인하여 p2의 부모가 블랙이면 특성 만족. p2의 부모가 레드이면 특성3이 위반되어 처음과 같은 문제가 발생한다. 이것은 x에 대해서 발생했던 문제와 같은 문제가 p2에 대해서 발생한 것이므로 p2를 문제 발생 노드로 하여 재귀적으로 재시작한다.

 

[Case 2] s가 블랙

[Case 2-1] x가 p의 오른쪽 자식

p를 중심으로 왼쪽으로 회전. 여전히 특성3을 위반하므로 Case 2-2를 적용

[Case 2-2] x가 p의 왼쪽 자식

p2를 중심으로 오른쪽으로 회전하고 p와 p2의 색상을 맞바꾼다.

 

시간복잡도

Case 1: logn(최악)

Case 2-1, 2-2: 상수 시간 내

 

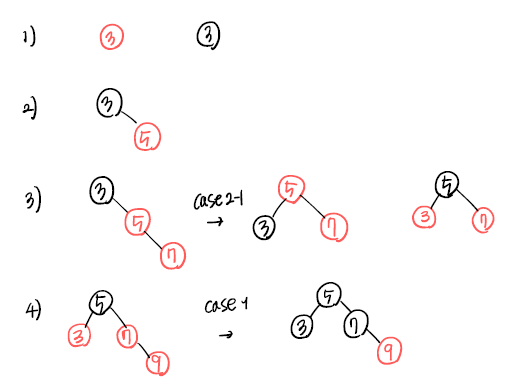
[예제] 빈 레드 블랙 트리에 다음 키들을 순서대로 삽입하시오. (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)

레드블랙트리의 삭제

삭제 노드의 자식이 없거나 1개만을 가진 노드로 제한해도 된다

삭제 노드를 m이라 하자

 

(1) 삭제 노드가 레드인 경우 그냥 삭제하고 자식을 이어붙인다.

(2-1) 삭제 노드가 블랙인 경우 유일한 자식이 레드이면 자식을 블랙으로 바꾸면 된다.
(2-2) 삭제 노드가 블랙인 경우 자식도 블랙이면 레벨이 부족하게 된다. (-1)

해결 방법은 x(m의 자식 트리 루트)의 주변 상황에 따라 다르다.

(3) 삭제 노드의 자식이 2개인 경우 삭제 노드의 색상 상관없이 직후원소찾아서 삭제할 노드를 대체한다. 직후원소가 비었으므로 직후원소의 자식 트리를 이어 붙인다. 이 경우 직후원소를 삭제된 것으로 판단하여 (1), (2), (3) 중 실행.

 

2-2 문제 발생의 경우의 수(총 7가지 -> 총 5가지)

m을 삭제하고 m의 자식이 p의 자식으로 연결된다.

p의 색에 따라서 Case 1(p레드)과 Case 2(p블랙)으로 나눈다.

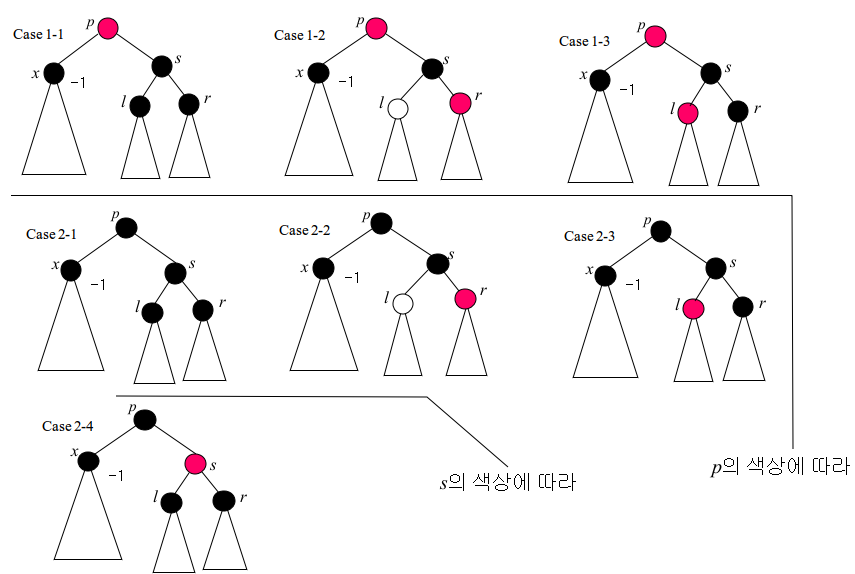
Case 1(p가 레드 / s는 반드시 블랙 / l과 r의 색상에 따라)

Case 1-1 <s블랙, l블랙, r블랙>

Case 1-2 <s블랙, l레드, r레드 or l블랙, r레드> == <l*, r레드>

Case 1-3 <s블랙, l레드, r블랙>

Case 2(p가 블랙 / s는 레드 or 블랙 / s와 l과 r의 색상에 따라)

Case 2-1 <s블랙, l블랙, r블랙>

Case 2-2 <s블랙, l레드, r레드> or <s블랙, l블랙, r레드>

Case 2-3 <s블랙, l레드, r블랙>

Case 2-4 <s레드, l블랙, r블랙> ※s가 레드이므로 l과 r은 반드시 블랙

 

이 경우 Case 1-2와 Case 2-2는 p의 색상만 다른데 p의 색상이 처리방법에 영향을 미치지 않으므로 통합한다.

이 경우 Case 1-3과 Case 2-3도 마찬가지로 통합한다.

 

최종적으로, Case 1-1, Case *-2, Case *-3, Case 2-1, Case 2-4로 총 5가지 경우의 수가 나온다.

 

각 Case 별 해결 방법 (5가지 모두 특성 4(블랙 레벨)를 위반한다)

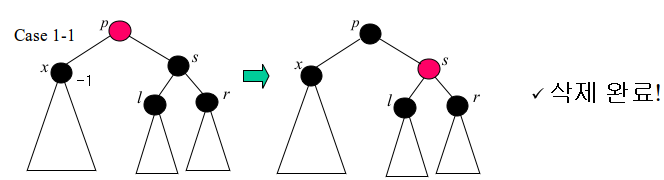
Case 1-1 <s블랙, l블랙, r블랙>

단순히 p와 s의 색상을 맞바꾼다. 해결된다.

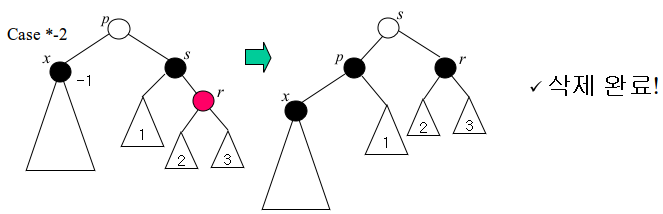
Case *-2

p를 중심으로 왼쪽으로 회전하고 p와 s의 색상을 맞바꾸고 r의 색상을 레드->블랙으로 바꾼다.

x에 이르는 블랙 레벨이 1 추가되었으므로 해결된다.

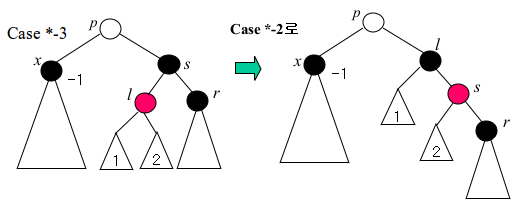
Case *-3.

s를 중심으로 오른쪽으로 회전하고 l과 s의 색상을 맞바꾼다. Case *-2로 이동한다.

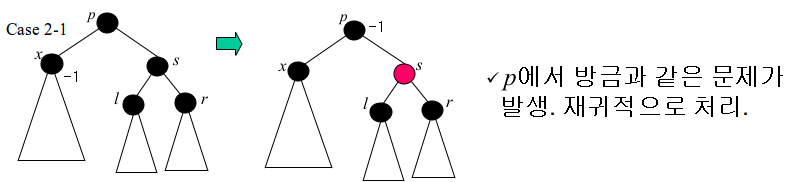
Case 2-1

s의 색상을 블랙->레드로 바꾼다. 이제 s를 지나는 경로에서도 블랙 노드가 하나 모자라게 되어 p를 지나는 경로 전체에서 블랙 노드가 하나 모자라게 된다. p를 문제발생노드로 하여 재귀적으로 다시 시작한다.

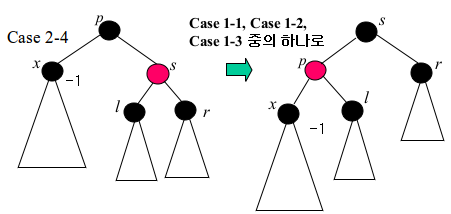
Case 2-4

p를 중심으로 왼쪽으로 회전시키고 p와 s의 색상을 맞바꾼다. l과 r을 경유하는 경로와 관련해서는 문제가 없다.

다만 문제가 발생한 x의 부모 노드p의 색상이 블랙에서 레드로 바뀌었는데 이것은 Case 1에 해당하여 색상의 조합을 따져 Case 1-1, 1-2, 1-3중 하나도 이동한다.

 

시간복잡도

레드블랙트리의 검색 알고리즘 : O(logn)

레드블랙트리의 삽입 알고리즘 : Case 1 = O(logn), Case 2 = 상수

레드블랙트리의 삭제 알고리즘 : O(logn)

삭제 알고리즘에서 삭제한 노드와 자식 루트가 블랙인 경우 5가지 Case에 대한 알고리즘 : 

Case 1-1, *-2, *-3, 2-4 = 상수 (Case 2-4는 Case 1-1, 1-2, 1-3중 하나로 이동하므로 상수 시간이다)

Case 2-1 = O(logn) 최악의 경우, 부모 노드에서 같은 상황이 다시 반복될 수 있고 최악의 경우, 루트 노드까지 올라갈 수 있기 때문이다

 

 

 

자료참조 - 쉽게 배우는 알고리즘 · 관계 중심의 사고법 / 문병로