[자료구조] 그래프 (Graph) 정의

그래프 Graph

그래프는 객체 간의 관계를 표현하는 자료구조입니다.

지도에서 지점들의 연결 상태, 도로망, 과목 선후수 관계, 전기회로의 소자 간 연결 상태, 사람들 간의 친분 관계 등을 그래프로 표현할 수 있습니다.

 

즉, 그래프란 현상이나 사물을 정점(vertex)과 간선(edge)로 표현한 것입니다.

그래프의 정의는 G = (V, E) 로 주어지며 V는 정점 집합, E는 간선 집합입니다.

정점(vertex)

객체를 의미하며 노드라고도 불립니다.

V(G) : 그래프 G의 정점들의 집합을 의미합니다.

간선(edge)

정점들간의 관계를 의미하며 링크(link)라고도 불립니다.

E(G) : 그래프 G의 간선들의 집합을 의미합니다.

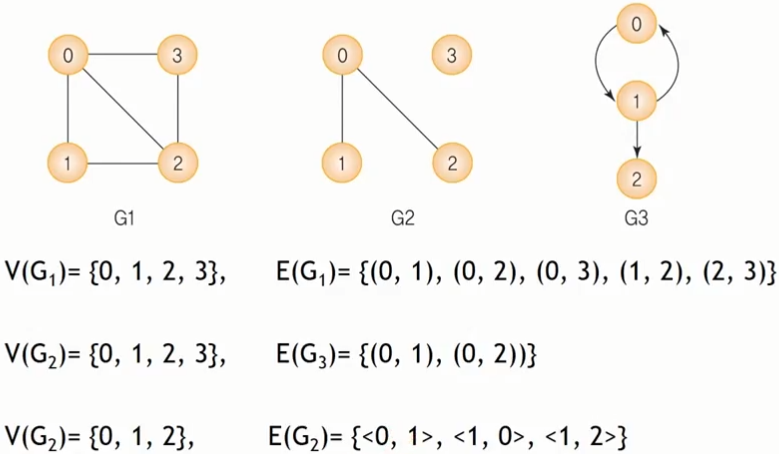
G1과 G2는 무방향 그래프, G3는 방향 그래프입니다. 방향성 존재 여부에 따라 집합 표현 방식이 다릅니다.

 

오일러 정리

모든 다리를 한번만 건너서 처음 출발했던 장소로 돌아오는 문제.

오일러가 발견한 문제에서는 간선의 수가 홀수인 것이 있으므로 답, 즉 오일러 경로가 존재하지 않았습니다. 따라서 오일러는 다음과 같이 정리하였습니다.

정리 : 각 정점에 인접한 간선의 수가 짝수이면 오일러 경로가 존재한다.

 

가중치 그래프(weighted graph)

간선에 비용이나 가중치가 할당된 그래프를 말합니다.

 

부분 그래프(subgraph)

정점 집합 V(G)와 간선 집합 E(G)의 부분 집합으로 이루어진 그래프를 말합니다.

인접한 정점과 간선

두 정점이 간선으로 직접 연결되어 있으면 인접하다고 할 수 있습니다.

G1

인접 정점(adjacent vertex) : 하나의 정점에서 간선에 의해 직접 연결된 정점

  G1에서 정점 0의 인접 정점 : 1, 2, 3

인접 간선(adjacent edge) : 하나의 정점에 직접 연결된 간선

  G1에서 정점 0의 인접 간선 수 : 3개

  G1에서 정점 1의 인접 간선 수 : 2개

 

무방향 그래프 차수(degree)

차수는 인접한 간선 수와 같습니다.

  G1에서 정점 0의 차수 : 3

  G1에서 정점 1의 차수 : 2

 

방향 그래프 차수(degree)

진입 차수(in-degree) : 들어오는 간선 수

진출 차수(out-degree) : 나가는 간선 수

G2

G2에서 정점 1의 진출 차수 : 2 | 진입 차수 : 1

방향 그래프의 모든 진입(진출)차수의 합은 간선 수와 같습니다.

G2의 진입 차수의 합 : 3

G2의 진출 차수의 합 : 3

G2의 간선 합 : 3

 

그래프의 경로(path)

그래프의 정점 S로부터 정점 T까지의 경로.

단순 경로(simple path)는 경로 중에서 반복되는 정점이 없는 경로입니다.

사이클(cycle)은 단순 경로의 시작 정점과 종료 정점이 동일한 경로입니다.

위 왼쪽 경로에서 0, 1, 2, 3은 단순 경로이며 0, 1, 3, 2는 경로가 될 수 없습니다. 또한 0, 1, 2, 1은 단순 경로가 아닙니다.

위 오른쪽 경로에서 0, 1, 2, 0은 시작 정점과 종료 정점이 동일하므로 사이클입니다.

 

연결 그래프(connected graph)

무방향 그래프 G에 있는 모든 정점 쌍에 대하여 항상 경로가 존재하는 그래프입니다.

왼쪽 : 연결그래프 오른쪽 : 연결그래프가 아님

완전 그래프(complete graph)

모든 정점이 연결되어 있는 그래프입니다.

n개의 정점을 가진 무방향 완전 그래프의 간선 수는 n(n - 1) / 2

정점이 4개라면, 간선 수는 6개이며 정점이 5개라면, 간선 수는 10개입니다.