[자료구조] 이진 탐색 트리 - 탐색, 삽입, 삭제 연산

이진 탐색 트리

이진 트리의 핵심입니다. 탐색 트리는 탐색 작업을 효율적으로 하기 위한 자료구조입니다.

루트 노드를 기준으로 왼쪽 서브 트리의 key값은 루트 노드보다 작고 오른쪽 서브 트리의 key값은 루트 노드보다 큽니다.

따라서 이진 탐색 트리를 중위순회하면 오름차순 정렬이 됩니다.

 

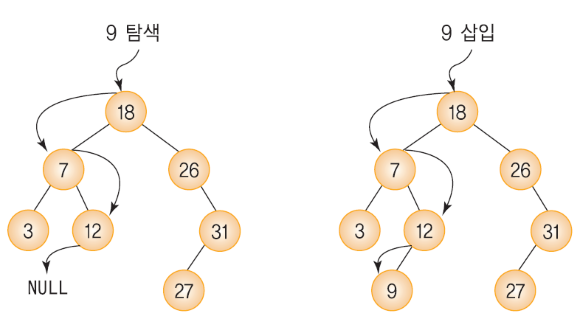
탐색 연산

주어진 키 값이 루트 노드의 키 값과 같으면 탐색에 성공합니다.

주어진 키 값이 루트 노드의 키 값보다 작으면 왼쪽 서브트리를 탐색합니다.

주어진 키 값이 루트 노드의 키 값보다 크면 오른쪽 서브트리를 탐색합니다.

 

이진탐색트리에서의 탐색을 구현하는 방법으로는 순환적 방법과 반복적 방법이 있습니다.

 

순환적인 탐색 함수

TreeNode  *search(TreeNode  *node,  int  key)
{
      if ( node == NULL )  return NULL;
      if ( key == node->key ) return node;
      else if ( key < node->key )
            return  search(node->left, key);  
      else
            return  search(node->right, key);
}

반복적인 탐색 함수

TreeNode *search(TreeNode *node, int key) 
{ 
	while(node != NULL){ 
	 	if( key == node->key ) return node; 
	 	else if( key < node->key ) 
			node = node->left; 
	 	else 
			node = node->right; 
	} 
	return node; 	// 탐색에 실패했을 경우 NULL 반환
} 

 

 

삽입 연산

이진 트리에 데이터를 삽입하는 연산을 위해서는 먼저 탐색 연산이 필요합니다. 삽입 하려는 데이터가 이미 존재하는 경우 삽입을 할 수 없기 때문입니다. 

따라서 탐색에 실패한 그 위치가 삽입할 위치가 됩니다.

TreeNode * new_node(int item)  {
	TreeNode * temp = (TreeNode *)malloc(sizeof(TreeNode));
	temp->key = item;
	temp->left = temp->right = NULL;
	return temp;
}

TreeNode * insert_node(TreeNode * node, int key){
	// 트리가 공백이면 새로운 노드를 반환한다. 
	if (node == NULL) return new_node(key);

	// 그렇지 않으면 순환적으로 트리를 내려간다. 
	if (key < node->key)
		node->left = insert_node(node->left, key);
	else if (key > node->key)
		node->right = insert_node(node->right, key);

	// 변경된 루트 포인터를 반환한다. 
	return node;
}

첫 if문에서 node가 NULL인 경우는 (1) 처음부터 트리가 NULL 포인터였거나 (2) 순회를 통해 삽입 가능한 위치를 발견한 경우입니다. 이 두가지 케이스에서 새로운 노드를 만들어내게 됩니다.

두번째 if문과 else if 문은 탐색을 하는 과정이며 재귀적 호출을 통해 삽입할 위치를 찾게 됩니다. 삽입을 완료하면 마지막 return문에서 변경된 루트 포인터를 반환합니다.

 

 

삭제 연산

삭제 연산은 탐색 연산과 삽입 연산에 비해 비교적 까다로운 알고리즘입니다. 

우선 삭제하는 경우는 다음 세가지 수가 존재합니다.

 

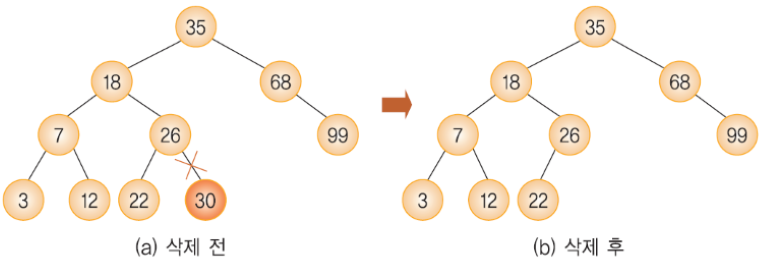
삭제할 노드가 (1) 단말 노드인 경우

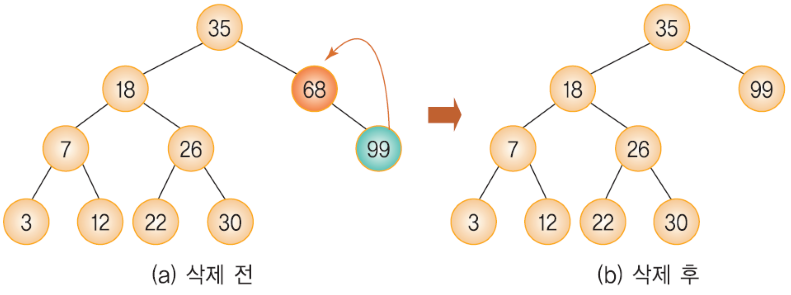
삭제할 노드가 (2) 하나의 서브트리만 가지고 있는 경우

삭제할 노드가 (3) 두 개의 서브트리를 가지고 있는 경우

 

(1) 단말 노드인 경우

단말 노드의 부모 노드를 찾아서 연결을 끊으면 됩니다.

(2) 하나의 서브트리만 가지고 있는 경우

해당 노드를 삭제하고 서브 트리를 부모 노드(삭제된 위치)에 붙여준다.

(3) 두 개의 서브트리를 가지고 있는 경우

삭제할 노드와 가장 근사한 값을 가진 노드(직후 노드 또는 직전 노드)를 삭제할 노드 위치로 가져옵니다.

 

TreeNode * min_value_node(TreeNode * node)
{
	TreeNode * current = node;
	// 맨 왼쪽 단말 노드를 찾으러 내려감
	while (current->left != NULL)
		current = current->left;
	return current;
}
TreeNode * delete_node(TreeNode * root, int key)  { // key 노드 삭제 후 루트 반환
	if (root == NULL) return root;
	if (key < root->key) 			// 키가 루트보다 작으면 왼쪽 서브 트리에 있음
		root->left = delete_node(root->left, key);
	else if (key > root->key) 		// 키가 루트보다 크면 오른쪽 서브 트리에 있음
		root->right = delete_node(root->right, key);
	else {				// 키가 루트와 같으면 이 노드를 삭제함
		if (root->left == NULL) {	// (1) or (2)
			TreeNode * temp = root->right;
			free(root);
			return temp;
		}
		else if (root->right == NULL) {	// (1) or (2)
			TreeNode * temp = root->left;
			free(root);
			return temp;
		}

		TreeNode * temp = min_value_node(root->right); 		// (3)
		root->key = temp->key; 				// 직후 키 복사
		root->right = delete_node(root->right, temp->key); 	// 직후 노드 삭제
	}
	return root;
}

 

 

연습문제

다음 이진 트리에서 노드 11을 삭제한다고 하였을 때 삭제 함수를 통한 연산 과정을 설명하라.

              11

    6                   19

4      8           17       43

  5      10              31    49

int main(void) {
	TreeNode* root = NULL;
	TreeNode* tmp = NULL;
	root = insert_node(root, 11);
	root = insert_node(root, 6);
	root = insert_node(root, 8);
	root = insert_node(root, 19);
	root = insert_node(root, 4);
	root = insert_node(root, 10);
	root = insert_node(root, 5);
	root = insert_node(root, 17);
	root = insert_node(root, 43);
	root = insert_node(root, 49);
	root = insert_node(root, 31);
	delete_node(root, 11);
    
    return 0;
}

1 | delete_node(root, 11)이 실행되면 key값이 바로 일치하므로 else문으로 진입한다. 

2 | 양쪽 서브트리가 모두 존재하므로 케이스 (3)에 해당하여 조건문을 들어가지 않으며 노드 포인터 temp에 min_value_node(root->right)에 대한 반환값을 넣는다.

3 | min_value_node 함수의 매개변수로 11의 오른쪽 서브트리인 19(*정확히는 19가 아니라 19를 key값으로 가진 루트 포인터이다)를 보내며 19의 이진트리에서 최솟값인 17을 반환한다. temp에는 17이 들어있다.

4 | 현재 루트의 key값 11을 temp의 key값인 17로 변경한다.

5 | 17의 오른쪽 서브트리인 19에 자식 노드 17이 아직 삭제되지 않았으므로 재귀 호출하여 19의 자식 노드 17을 제거한다.

6 | 변경된 루트 17을 반환한다