1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
1707. 이분 그래프
접근한 방법
까다로운 테스트케이스, 조건들이 많아서 풀기에 꽤 재미있었던 문제. 이분그래프는 개념만 보면 한번에 이해하기 어려울 수 있는데 그림으로 표현하면 쉽습니다.

정점을 1 또는 0으로 표현했을 때 같은 집합 안에서 1과 1이 인접하거나 0과 0인 정점이 인접하는 경우가 없다면 이분그래프입니다.
이 그림에서는 왼쪽이 이분그래프, 오른쪽은 아닙니다.
이 아이디어 그대로 모든 정점을 1 또는 0으로 표시해놓을 표시용 배열(코드에서는 marks)을 만들어놓고 bfs탐색을 들어가서 자신과 연결되어 있는 정점들을 자신과 반대되도록 표시하면 됩니다.
만약 표시를 하려고 하는데 현재 정점과 동일한 마크가 표시되어 있다면 그 그래프는 이분그래프가 아닌게 됩니다. 오른쪽 그림에서 정점 3과 4가 표시되어있고 정점 5를 탐색하는 경우가 해당합니다.
주의해야할 점은 문제에서 주어지는 테스트케이스는 모든 정점이 연결된다는 것을 보장하지 않는다는 것인데 예를 들면 아래와 같은 그래프들입니다.
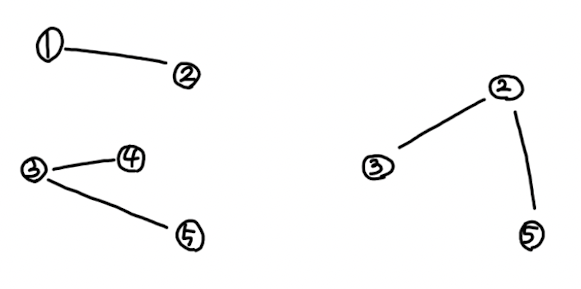
둘다 이분 그래프이고 왼쪽은 2와 4가 연결되어 있지 않으며 오른쪽은 1, 4에 대한 간선 정보가 없습니다.
그러므로 어느 한 정점에서만 탐색을 해서는 안되고 우선 연결되어 있는 정점 하나를 찾아서 탐색을 한 후에 아직 표시되지 않은 정점이 있다면 그 정점으로부터 다시 탐색을 시작해야 합니다. 이 부분은 표시용 배열의 참조를 유지하면서 탐색하면 됩니다.
Python
import sys
input = sys.stdin.readline
n = int(input())
def bfs(s, marks):
from collections import deque
q = deque()
q.append((s, True))
marks[s] = True
while q:
now, m = q.popleft()
for v in graph[now]:
if marks[v] == m:
return False
elif marks[v] == -1:
marks[v] = not m
q.append((v, not m))
return True
for i in range(n):
v, e = map(int, input().split())
graph = [[] for _ in range(v + 1)]
marks = [-1] * (v + 1)
for i in range(e):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
result = "YES"
for i in range(1, v + 1):
if not graph[i]:
continue
if marks[i] == -1:
if not bfs(i, marks):
result = "NO"
break
print(result)JavaScript
function solution(v, e, edges) {
const bfs = (s, marks) => {
const q = [[s, true]];
let front = 0;
marks[s] = true;
while (q[front]) {
const [now, m] = q[front++];
for (const v of graph[now]) {
if (marks[v] === m) return false;
else if (marks[v] === -1) {
marks[v] = !m;
q.push([v, !m]);
}
}
}
return true;
};
const graph = Array.from({ length: v + 1 }, () => []);
const marks = Array(v + 1).fill(-1);
edges.forEach((edge) => {
const [a, b] = edge;
graph[a].push(b);
graph[b].push(a);
});
let result = "YES";
for (let i = 1; i <= v; i += 1) {
if (graph[i] && marks[i] === -1 && !bfs(i, marks)) {
result = "NO";
break;
}
}
return result;
}
solution(4, 4, [[1, 2], [2, 3], [3, 4], [4, 2]])
solution(5, 4, [[1, 2], [3, 4], [3, 5], [4, 5]])
solution(5, 3, [[2, 4], [3, 5], [4, 5]])'알고리즘 테스트 ⏲ > 백준' 카테고리의 다른 글
| [백준] 1339. 단어 수학 풀이 (Python, JavaScript) (0) | 2023.07.06 |
|---|---|
| [백준] 14502. 연구소 풀이 (Python, JavaScript) (0) | 2023.07.05 |
| [백준] 16947. 서울 지하철 2호선 풀이 (Python, JavaScript) (0) | 2023.06.21 |
| [백준] 16919. Two Dots 풀이 (Python, JavaScript) (0) | 2023.06.20 |
| [백준] 5014. 스타트링크 풀이 (Python, JavaScript) (0) | 2023.06.16 |