에라토스테네스의 체 (Sieve of Eratosthenes)
소수는 1보다 큰 자연수 중 1과 자기자신만을 약수로 가지는 수입니다. 특정한 자연수가 소수인지 아닌지는 다음과 같은 간단한 알고리즘을 통해 판별할 수 있습니다.
// 소수 판별 O(N^(1/2))
#include <iostream>
using namespace std;
bool isPrime(int x) {
int rt = (int)sqrt(x);
for (int i = 2; i <= rt; i++)
if (x % i == 0) return false;
return true;
}
int main() {
int x; cin >> x;
cout << boolalpha << isPrime(x);
}예를 들어 자연수 17은 약수가 1과 17이므로 소수입니다.
위 식의 경우 수가 소수인지 아닌지를 한번씩만 확인할 수 있습니다. 그렇다면 매우 많은 자연수들을 깔아놓고 한번에, 동시에 소수를 판별하고 싶다면 어떤 방법을 사용하면 될까요.
이러한 경우에 사용되는 것이 `에라토스테네스의 체` 입니다.
이 개념은 고대 그리스 수학자 에라토스테네스가 발견한 소수를 찾는 방법입니다.
기본적인 알고리즘은 다음과 같습니다.
(1) 2부터 구하고자 하는 수를 나열한다.
(2) 2의 배수를 제거한다. (자기 자신은 제외)
(3) 3의 배수를 제거한다. (자기 자신은 제외)
(4) 5의 배수를 제거한다. (자기 자신은 제외)
(5) 7의 배수를 제거한다. (자기 자신은 제외)
이미 제거된 수는 건너뛰므로 4와 6 등은 건너뛰게 됩니다. 이 과정을 반복하여 제거되지 않고 남은 수들은 모두 소수가 됩니다.
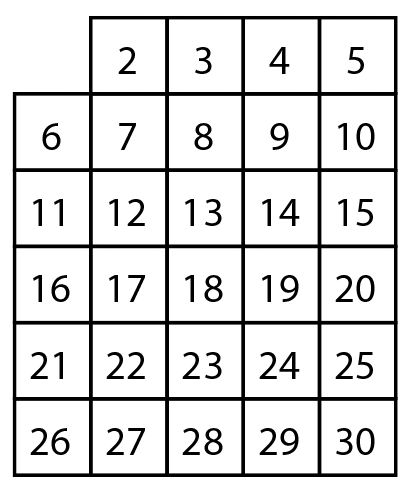
위 2차원 배열을 에라토스테네스의 체를 이용해 소수를 판별해보겠습니다.
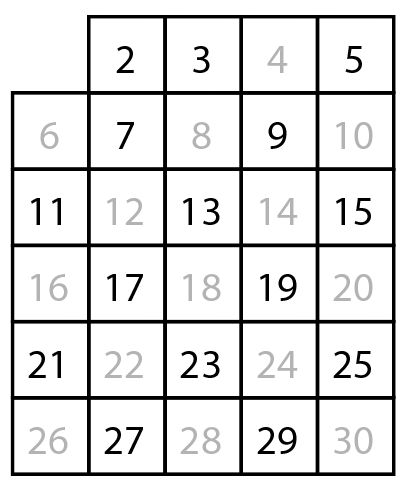
먼저 자기자신을 제외하고 2의 배수를 제거합니다.
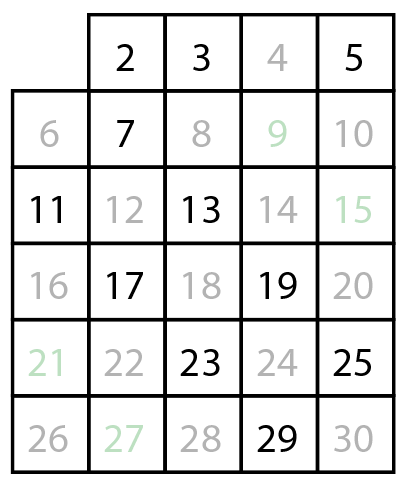
자기자신을 제외하고 3의 배수를 제거합니다. 4는 제거되어 있으므로 건너뜁니다.
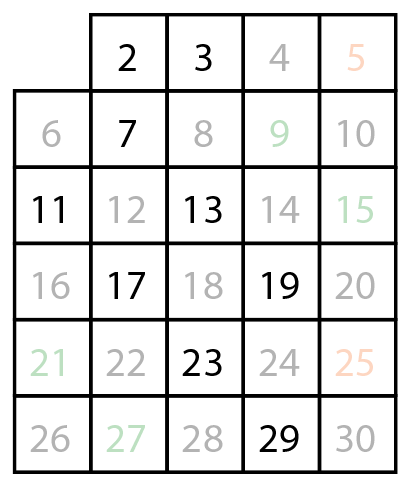
자기자신을 제외하고 5의 배수를 제거합니다. 이 과정을 반복하여 결과적으로 위와 같이 제거되지 않은 2, 3, 7, 11, 13, 17, 19, 23, 29가 소수가 됩니다.
알고리즘 구현
// Algorithm Analysis
// 에라토스테네스의 체 (Sieve of Eratosthenes)
#include <iostream>
using namespace std;
int num = 10000; // 2~10000까지의 소수 판별
int arr[10001];
void sieveOfEratos() {
// 2부터 num까지 초기화
for (int i = 2; i <= num; i++) {
arr[i] = i;
}
// 배수 제거
for (int i = 2; i <= num; i++) {
if (arr[i] == 0) continue; // 이미 제거되었으면 건너뜀
for (int j = i * 2; j <= num; j += i) { // 자기자신 제외하고 제거
arr[j] = 0; // 제거
}
}
for (int i = 2; i <= num; i++) {
if (arr[i] != 0) cout << arr[i] << " ";
}
}
int main() {
sieveOfEratos();
}
실행결과는 다음과 같습니다.

* 나동빈님 블로그를 참고하여 개인적으로 재작성한 글입니다.
'컴퓨터공학 💻 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm) (0) | 2021.07.15 |
|---|---|
| [알고리즘] 데이크스트라 알고리즘 (Dijkstra Algorithm) (0) | 2021.07.14 |
| [알고리즘] 다이나믹 프로그래밍 (Dynamic Programming) (0) | 2021.07.12 |
| [알고리즘] 크루스칼 알고리즘 (Kruskal Algorithm) (0) | 2021.07.10 |
| [알고리즘] 합집합 찾기 알고리즘 (Union-Find) (0) | 2021.07.10 |